T.C.İSTANBUL ÜNİVERSİTESİ SOSYAL BİLİMLER ENSTİTÜSÜ FELSEFE ANABİLİM DALIYÜKSEK LİSANS TEZİ
DERİN ÖĞRENMENİN FELSEFİ TEMELLERİ
GÜLNİHAL PEHLİVAN
2501140185
TEZ DANIŞMANI
DOÇ. DR. ÖZGÜÇ GÜVEN
İSTANBUL-2019
ÖZET
DERİN ÖĞRENMENİN FELSEFİ TEMELLERİGÜLNİHAL PEHLİVAN
Çalışmamızın temel amacı yapay zekâ başlığı altında insan beynini model alan derin öğrenmenin gelişim sürecini inceleyerek anlamlı bir bütün oluşturmak ve yeni bir öngörü ortaya koymaktır. Bu amaçla ilk bölümde tarih boyunca matematikalanında ortaya çıkan, makinelere duyulan ihtiyacın ne şekilde ilerlediği ele alınmıştır. İkinci bölümde, yapay zekâ alanında önemli öngörülerde bulunmuş olan Alan Turing’in “Hesaplama Makineleri ve Zekâ” isimli makalesi incelenmiştir. Ardından Turing’in öngörülerine farklı bir açıdan yaklaşan J. Searle’ün Çin Odası Deneyi ve bilinç tartışmasına yer verilmiştir. Son bölümde ise makine öğrenmesi kavramı, derin öğrenme ve yapay sinir ağları bağlamında incelenmiştir. İnsan beyninin yapısı model alınarak geliştirilen yapay sinir ağları ve derin öğrenmenin mimari yapılarındaki gelişim değerlendirilmiştir. Bu alanda şimdiye kadar yapılmış olan çalışmalardan yola çıkılarak düzeltilebilecek hatalar ve bundan sonrası içingidilebilecek yeni yollar ortaya konulmuştur.
ÖNSÖZ
Matematik bölümünde tamamladığım lisans öğrenimim boyunca teori ve ispatlar üzerinde yaptığımız çalışmalarımızın kullanım alanlarına olan merakım, beni teorik olarak öğrendiğim matematiği pratik olarak uygulayabileceğim yazılım alanına yönlendirdi. Aldığım yazılım eğitimi ve özel sektörde edindiğim programlama deneyimim sırasında bu alanda ne kadar ileri gidilebileceği konusu ile ilgilenmeye başladım. Yazılım alanında gidilebilecek en ileri noktanın kendi kendini programlayabilen/geliştirebilen bir program olduğunu düşündüm. İnsanın bilişsel yetenekler ediniminde önemli bir rol oynayan öğrenme sürecinin makineler için farklı şekillerde işleyen makine öğrenmesi yöntemleriyle karşılık buluşunu ve bu tekniklerin farklı alanlarda kullanım örneklerini inceledim. Bu öğrenme yöntemlerinin insandan elde edilen eğitim verileri olmadan çok daha başarılı sonuçlara ulaşması ile makinelerin başarılı olamayacağı öngörülen birçok alanda başarı göstermiş olması bu alana olan merakımı arttırdı. Bu alanda yapılan çalışmaların sağlam temeller üzerinde ilerleyebilmesi ve doğru soruların sorulabilmesi için hesap makinelerinden başlayarak bilgisayar teknolojisindeki tüm bu tarihi sürecin felsefi bir bakış açısıyla ele alınmasının faydalı olacağını düşünerek araştırmalarıma başladım.
Matematik felsefesi alanında ilerlemek için başladığım yüksek lisans öğrenimim araştırmalarım için yol gösterici oldu. Yüksek lisans ders döneminde aldığım matematik felsefesi dersiyle genel olarak matematiksel bilginin doğasına ilişkin yeni sorularım oluştu. Sorularım sayesinde bilgisayarların -dolayısıyla yapay zekânın- matematiksel mantık ile matematiğin sınırları ve gücü hakkındaki felsefi sorunları aydınlatmak için ortaya çıkmış olduğunu gördüm. Böylece günümüzde enileri yapay zekâ teknolojisi olarak kabul edilen derin öğrenmenin gelişim sürecini felsefe yardımıyla araştırmayı ve bu çalışma alanına katkı sağlayabilmeyi amaçedindim. Bu konuya olan ilgi ve merakımın artmasının nedenlerinden biri de matematik felsefesi dersini, değerli hocam Doç. Dr. Özgüç Güven gibi işine değer katarak yapan birinden almış olmamdır. Tez yazma sürecimde yönlendirmeleri ve tezime yaptığı katkılarından dolayı saygıdeğer tez danışmanın Doç. Dr. Özgüç Güven’e ve tez içeriği ile ilgili düzeltme ve yönlendirmelerinden istifade ettiğim Dr. Öğr. Üyesi Vedat Kamer’e teşekkürü bir borç bilirim.
Tez süresince fizik alanında tüm sorularımı sabırla yanıtlayan sevgili kuzenimDr. Özlem Pehlivan’a ve hayatım boyunca her zaman bana destek olan ailemesonsuz teşekkür ederim.
GÜLNİHAL PEHLİVAN
İSTANBUL, 2019.
GİRİŞ
Felsefe tarihi boyunca insanın düşünce sistemi, beyin yapısı, öğrenme mekanizması, hayatı algılayışı felsefecilerin üzerinde durduğu konular olmuştur. Sokrates, Platon ve Aristoteles insanın düşünce sistemi, dil yeteneği, beyin ve zihin kavramları üzerinde araştırmalar yapmış ve fikir üretmişlerdir. Ancak bu konularda bilimsel ve teknolojik açıdan önemli ilerlemeler 19. yüzyılın sonlarında yaşanmıştır. Matematik dünyasında bir eşik noktası kabul edilen; matematiği formelleştirme çalışmaları ve bu bağlamda Hilbert’in ortaya attığı sorular, algoritmik işlemleri temsileden matematiksel kavramların ve bu kavramlarla çalışabilen soyut makinelerin geliştirilmesiyle sonuçlanmıştır. Bu matematiksel yaklaşımların en genelleştirilmiş hali 1937'de Alan M. Turing tarafından ortaya atılan Turing makineleridir. Turing bu buluşundan sonra insan zekâsının taklit edilebilirliği üzerinde düşünmüş ve bu düşüncelerini 1950 yılında yayınlanan Hesaplama1 Makineleri ve Zekâ (Computing Machinery and Intelligence) makalesiyle ortaya koymuştur. Turing bu makalesinde insan zekâsının makinelerle taklit edilip edilemeyeceğini, makinelerin bir zekâya sahip olup olamayacağını, düşünüp düşünemeyeceğini sormuş ve bu sorularüzerinden kendi görüşlerini açıklamış ve karşıt görüşleri de değerlendirmiştir.
1 Burada dilimize “hesaplama” olarak çevrilen “calculate” ve “compute” kelimeleri arasındaki anlam farkını irdeleyebiliriz. Anlam farkını anlamanın en kolay yolu bu kelimelerden türetilmiş kelimelere bakmaktır: “calculator” (hesap makinesi) ve “computer” (bilgisayar). Basit aritmetik işlemleri yapmakiçin kullanılan araç olan hesap makinesi ve genellikle karmaşık algoritmalar içeren karmaşık işleri yapmak için kullanılan bilgisayar kelimeleri farklı anlamlar içeren kelimelerdir. Bu nedenle sadelik içeren işlemleri hesaplamayı belirtmek için “calculate” ve “calculation” kelimelerini ve karmaşıklık içeren işlemlerin hesaplanmasını belirtmek için “compute” ve “computation” kelimeleri kullanılır.Ayrıca bkz. Maryanne Cline Horowitz, New Dictionary of the History of Ideas, Charles Scribner's Sons, 2005, s. 255.
Turing’den sonra insan beyninin fonksiyonlarının makineler tarafından taklit edilebileceği düşüncesi yeni hedefler belirlenerek ilerlemiştir. İnsanların ve makinelerin sınırları, neleri yapabilecekleri, neleri yapamayacakları gibi konular tartışılmıştır. Böylece günümüzde yapay zekâ, bilgisayar bilimlerinin bir alt dalı gibi görülmektedir fakat konusu ne olursa olsun bütün bilimlerin ortaya koyduğu çalışmalar yapay zekânın gelişimine katkı sağlayan çalışmalar olarak kabul edilmektedir.
Yapay Zekâ’nın çalışma alanlarından biri olan Makine Öğrenmesi ise bilgisayarların kodlar aracılığı ile komut almasının yanında veri kümelerinden de öğrenerek çıkarımlar yapmasını sağlar. Bir makine öğrenmesi tekniği olan derin öğrenmede ise insan beynindeki sinir ağları örnek alınarak oluşturulan yapay sinir ağları ile işlemler gerçekleştirilir. Derin öğrenmenin gelişimi, diğer teknolojik gelişmelerle de ilişkilidir örneğin fotoğraflardaki ve videolardaki çözünürlüğün ve kullanılan GPU (Grafik İşleme Birimi) performansının artması derin öğrenme tekniğinin işlevselliğini arttırmıştır.
Çalışmamızda derin öğrenmenin felsefi temellerini inceleyebilmek için öncelikle makinelerin tarihi gelişimine yer vereceğiz. Birinci bölümde ilk hesapmakinelerinden günümüz bilgisayarlarına uzanan bu süreci ve makinelerin yapabileceklerine dair ortaya atılan fikirleri inceleyeceğiz. Makinelerin hesaplamaişlerinde kullanımının yaygınlaşması ile oluşan fikirlerden biri Leibniz’in tüm düşünme işlerini makinelere yaptırma fikridir. Buna göre Leibniz günlük hayatta yaşanan tüm tartışmaların, matematiksel işlemlerde olduğu gibi sembolik bir şekilde makinelere aktarılması bu yol ile kesin ve net bir şekilde tek bir sonuca ulaşılmasını, insanlar arasında yaşanan anlaşmazlıkların böylece son bulmasını hayal etmiştir. Leibniz’in evrensel dil fikri onun hedeflediği şekilde gelişmese de, onun çalışmaları üzerinden mantık ve biçimsel diller geliştirilmiş bu yolla günümüzde iletişim ve bilgiye erişim çok daha kolay hale gelmiştir.
Bilgisayarların tarihi gelişim süreci incelendikten sonra Turing’in bilgisayarların düşünebilme yeteneğini sorguladığı “Hesaplama Makineleri ve Zekâ” makalesine yer vereceğiz. Bu makale üzerinden Turing’in “Bilgisayarlar düşünebilir mi?” sorusuna eş değer olarak önerdiği taklit oyununu ele alacağız. Ardından bu konu ile ilgilieleştirileri tartıştığı ikinci bölümden yola çıkarak günümüz teknolojisi ve bakış açısıyla Turing’in görüşlerini inceleyeceğiz. Sonrasında Turing’in görüşlerini eleştiren John Searle’ün Çin odası deneyi üzerinden bilinci tartışacağız.
Son bölümde ise makine öğrenmesi teknikleri ve yapay sinir ağları ilegeliştirilen derin öğrenmenin ne olduğunu ve nasıl çalıştığını ele alacağız. Derinöğrenmenin yapısal özelliklerini inceledikten sonra bilinci açıklama iddiasıyla hâlihazırda sürdürülen Mavi Beyin Projesi’nden söz edeceğiz. Son olarak beynin modellenmesi ve modellenen bu beyinde bilincin oluşmasına ilişkin görüşlere yervereceğiz.
BİRİNCİ BÖLÜM
HESAPLAMA MAKİNELERİNİN TARİHİ
Beyindeki yapı ve işlevler örnek alınarak tasarlanmış olan yapay sinir ağları üzerinde çalışan; algoritma ve modeller derin öğrenme denilen çalışma alanını oluşturur. Derin öğrenmenin felsefi temellerini inceleyebilmek, bu alanda bugünyapılan çalışmaları anlayabilmek ve bu gelişim içinde ortaya çıkan sorunlara değinebilmek için öncelikle makinelerin gelişim sürecinden bahsedeceğiz.
1.1 İlk Hesap Makineleri
İlk hesap makineleri olarak bilinen abaküslerin bundan 3000 yıl önce kullanıldığı tahmin edilmektedir. Mekanizması el ile çalıştırılan ilk hesap makinesini ise Blaise Pascal (1623-1662) geliştirmiştir. 2
2 Georges Ifrah, Rakamların Evrensel Tarihi: Akdeniz Kıyılarında Hesap, Tubitak, 1995, s. 109.
Pascal 1642'de, babasının ticari hesapları için ona yardımcı olacak bir hesap makinesi yapmıştır. Pascal’ın geliştirdiği makinenin mekanizması, bir kutunun kapağındaki pencerelerden pozisyonları görülebilen bir sayı tekerleği dizisinden oluşmuştur. 3 Bu makine sayesinde hesaplanacak numaralar seçiliyor ve dişli çarklar döndürülerek, verilen iki sayı üzerinde toplama ve çıkarma işlemleri gerçekleştirilebiliyordu. Pascaline olarak bilinen bu makine 1645’ten bugüne Paris Sanat Müzesi’nde sergilenmektedir.
3 Gerard O'Regan, A Brief History of Computing, Springer Science- Business Media, 2012, s. 25.
1.1.1 Leibniz’in Hayâli
1671’de ise Gottfried Wilhelm Leibniz (1646-1716) sadece toplama veçıkarmayı değil dört aritmetik işlemin dördünü de yapabilecek bir makinegeliştirmek için çalışmalar yapmıştır. 4 Leibniz aynı zamanda dört işlemi yapabilen buluşunun uzun vadedeki sonuçlarına, getirebileceği yenilik ve kolaylıklara da odaklanmıştır. Hesap makinesini tamamladıktan sonra hesaplama gibi uzun ve yorucu bilişsel bir işin, makinelere yaptırılabildiğini görmüş ve insan akıl yürütüşünün önemli bir kısmının da hesaplamalara indirgenebileceğini düşünmüştür. Böylece akıl yürütmelerimizi sembolik mantık ve matematik ile ifade edebildiğimiz gibi tüm akıl yürütmelerimiz için ortak bir ifade şekli olursa her şeyi mekanik olarak yani somutlaştırarak daha kolay çözebileceğimizi öngörmüştür.
4 Deborah J. Bennett, Logic Made Easy, W.W. Norton & Co, 2004, s.148.
Şekil 1 Leibniz’in dört işlem yapan hesap makinesi (Deutsches Museum, Munich)5
Leibniz’in evrensel bir dil ve akılyürütme konusundaki hayali, kendi ünlü sözleriyle de şu şekilde özetlenmiştir:
“...Akılyürütmelerimizi arındırmanın tek yolu onları matematikçilerin ele aldığı gibi somutlaştırmaktır, böylelikle hatalarımızı tek bakışta bulabilir ve bireyler arasında anlaşmazlık çıktığında şunu söyleyebiliriz: Hadi hesaplayalım! [Calculemus!] Aceleye getirmeden kimindoğru olduğunu görebilmek için...”6
5 Edwin D. Reilly, Milestones in Computer Science and Information Technology, Greenwood Publishing Group, 2003, s. 152.
6 Gottfried Wilhelm Von Leibniz, G. W. Philosophical Essays (Çev: R. Ariew & D. Garber), Hackett Publishing Company, 1989, s. 5-10.
Bu söyleminde Leibniz’in, düşünme ve akılyürütme gibi işleri insanlar için yapabilecek bir makine sistemi hayâl ettiği görülmektedir. Leibniz bu sisteme “calculus ratiocinator” (akıl yürütmenin hesabı) adını vermiştir. Düşünme işlerini insanların yerine yapabilen böyle bir sistemin oluşturulması için Leibniz kendigeliştirdiği hesap makinesini örnek almıştır. Kendi tasarımı olan hesap makinesinde sayıların temsil edilişi gibi, düşüncelerde geçen kavramların da matematiksel olarak temsil edilebilmesini sağlayan sembolik bir dile gereksinim duymuştur. Buna göre Leibniz, doğruluk tartışmalarında duyusallıktan kaynaklanan düşünce ayrılıklarının son bulması için düşüncenin biçimselleştirilmesi gerektiğini savunmuştur. Düşüncenin önemli bir kısmını biçimselleştirmek için de, matematikte kullandığımız türden simgelerin ve kuralların gerektiğini öne sürmüştür.
Leibniz’in, “New Essays On Human Understanding” (Evrensel Bir Karakteristiğe Önsöz) başlıklı makalesinde açıkladığı gibi, characteristica universalis (evrensel dil) aracılığıyla düşüncelerimizin alfabesi ortaya çıkacak, temel kavramların analizi yapılabilecektir. Böylece insan düşüncesindeki her şey hesapsal olarak kesin bir şekilde yargılanacaktır. Öyle ki, iki farklı görüşü savunan kişilerin çatışmasına gerek kalmayacak; “calculemus” eş deyişle “buyurun hesaplayalım” dendiğinde kimin haklı olduğu hesaplanabilecektir. Böyle bir sistem inşa edildiğinde Leibniz’e göre, iki filozof arasında iki muhasebeciden daha fazla bir tartışma gerekmeyecektir.7 Burada geçen characteristica universalis düşüncesi de bir tür hesapsal formülleştirmedir. Eğer insan düşüncelerini tam anlamıyla ifade edebilecek karakterler bulunursa, aritmetik ve geometride yapılabilecek herhangi bir işlem bu semboller ile insan akılyürütmesi üzerinde de yapılabilecektir. Lebniz’e göre insan akıl yürütmesinde yapılabilecek tüm araştırmalar bu karakterlerle aktarılarak (transpose) ve bunun matematiğin bir kolu olması sağlanarak geliştirilebilir. Böylece karmaşık görünen akılyürütmeler, karakterler yoluyla basitleştirilebilir ve ifade edilebilir.
Leibniz karakteristik üzerine ilk yazılarında, cebir yerine evrensel bir dil ya da alfabe olduğunu düşünmekteydi. 1676’da düşüncenin cebirini kavradı, geleneksel cebiri ve onun simgesini de ekleyerek modelledi.
Leibniz’in böyle bir düşünceyi ortaya atmasındaki esas sebep; siyasi veya felsefi tartışma ve araştırmaların matematiksel bir yöntem izlemediğinin farkına varmasıydı. Leibniz’e göre, matematikçiler de hata yapabilir fakat bu hataların ne olduğunu fark etmelerini sağlayan yöntem/araçları da vardır; bu araçlara sahip olmayan felsefeciler ve siyasetçiler ise daha fazla hata yapabilirler.8
7 Gottfried Wilhelm Von Leibniz, New Essays On Human Understanding, (Der. P. Remmant J. Bennet), New York: Cambridge University Press, 1997, s. 282
8 Bekir S. Gür, Leibniz’in Matematik(sel) Düşüncesi, Matematik Dünyası, 2005 Güz, s. 91.
Leibniz, yaşamı boyunca Aristoteles’in kurduğu biçimsel mantığa büyük önem verir. Aristoteles’in kıyas teorisini, düşüncenin formüle edilişi bakımından önemli biradım olarak görür. Fakat Leibniz, characteristica universalis anlayışına uygun olarak insan düşüncesindeki her bileşeni hesapsal olarak kesin bir şekilde yargılamayı, Aristoteles mantığı üzerinden gerçekleştirmeye çalışsa da başarılı olamamıştır. Yine de Leibniz sembolik mantık konusunda ilk sistemli çalışmaları gerçekleştirmiş veİngiliz matematikçi George Boole'un (1815-1864) cebirsel mantık çalışmalarına da altyapı sağlamıştır.
1.2 İlk Mekanik Bilgisayar
19. yüzyılda, Newton ve Leibniz’in matematik alanında yaptığı çalışmalar ile birlikte, mühendislikte kullanılan bazı fonksiyonların yerine bu fonksiyonların yerini alabilen polinomların kullanılabileceği anlaşılmıştır. Charles Babbage (1791-1871) bu tür polinomlarla işlemleri gerçekleştirecek makineler tasarlamayı düşünmüştür. Leibniz’in icat ettiği dört işlem yapabilen hesap makinesinden sonra bilgisayar tarihindeki en büyük teknik ilerleme olarak Charles Babbage’ın bu tasarımları sayılabilmektedir; Fark Makinesi (Difference Engine) ve Analitik Makine (Analytical Engine).
Pascal’ın ve Leibniz’in hesap makineleri, Babbage'ın yapmayı planladığı hesaplama makinesinden önemli bir açıdan farklıydı, onlarınki elle işletilen (manuel) hesap makineleriydi, ama Babbage tasarımında makinenin otomatik olmasını planlamıştı. Pascal’ın ve Leibniz’in her aşamada dikkatli bir insan müdahalesi gerektiren çalışmalarının aksine Babbage’ın makineleri sonuçları otomatik olarak üretmek için tasarlanmıştı.
Babbage öncelikle, Cambridge Üniversitesinde matematik öğrencisi iken, denizcilikte çok fazla kullanılan matematik tabloları9 hesaplayıp, basan bir hesap makinesi fikrini ortaya atar. Bu dönemde matematik tablolar, hesaplama işinden sorumlu insanlarca hazırlanmaktaydı. Bu matematik tabloların oluşturulması kavramsal olarak zor değildi, fakat onları oluşturmak için yapılması gereken çok sayıda hesaplama ve bu hesaplamaları yaparken ortaya çıkan hatalar, Babbage'ın çok fazla zamanını alıyordu. Buna çözüm olarak Babbage, sayısal tabloları mekanik olarak ve dolayısıyla hatasız düzenleyebilecek bir makine üretmeye çalışmıştı.
9 Trigonometrik, logaritmik ve diğer fonksiyonların değerlerinin listelendiği kitaplara matematik tablolar denir. Astronomi, mühendislik, denizcilikte önemli bir kullanımı vardır.
Şekil 2. 1991’de Babbage’ın doğumunun 200. yılında fark makinesi tamamlandı ve çalıştırıldı.
(Londra Bilim Müzesi)10
Babbage’ın ilk tasarımı Fark Makinesi olmuştur. Bu makine teoride polinom fonksiyonları, girilen başlangıç değerlerine göre onluk tabanda hesaplayabiliyordu, bu hesaplama sırasında da çarpma ve bölme işlemlerini kullanmıyor sonlu farklar yönteminden11 faydalanıyordu.
Babbage, Fark Makinesi’ni yapabilmek için yeterli finansal desteği almış olmasına karşın onu tamamlayamadı.12 Bunun önemli bir nedeni de, Babbage’ın makinenin tasarımına sürekli yeni fikirler eklemek istemesi böylece tasarım sürecini asla tamamlayamaması, gösterilmektedir.13
10 Londra Bilim Müzesi resmi web sitesi fotoğraf veri tabanından (Çevrimiçi)https://collection.sciencemuseum.org.uk, 12 Aralık 2019.
11 Bu yöntemle sonlu fark denklemleriyle diferansiyel denklemlerin analitik çözümlerine yaklaşılır.
12 Fark Makinesi demir, bronz ve çelikten üretilmiş 4,000 parçadan oluşan 3 ton ağırlığında, 8 metregenişliğinde ve 4 metre yüksekliğinde bir makine olarak tasarlanmıştı ve 1800’lerde böyle bir tasarımın yapımı oldukça zordu. Ayrıca bkz. Gerard O'Regan, A Brief History of Computing, Springer Science- Business Media, 2012, s. 42.
13 Gerard O'Regan, a.g.e., s. 42.
Babbage, Fark Makinesi’nin özel amaçlara yönelik bir hesaplayıcı olmasından ötürü bir süre sonra daha işlevsel olan başka türde bir hesaplayıcı oluşturulabileceğini düşünür. Bu kez özel amaçlarla sınırlı olmayan daha genel amaçlar için, her formüle uygun “programlanabilecek” bir makine tasarlamaya başlar. Babbage, çok daha güçlü ve esnek bir makine üretilebileceğini fark ettiğinde Fark Makinesi’ne olan ilgisini kaybeder. Artık ilgisi Analitik Makine adını verdiği tasarıma yönelmiştir. Analitik Makine’nin mekanik yapısı, Fark Makinesi’nde kullanılan dişli sütunlarına benzer, ancak Fark Makinesi’nde yalnızca sekiz sütun varken, Analitik Makine’de 20.000 sütun olması gerekir.14 Babbage bir önceki projesiolan Fark Makinesi’ni tamamlayamamış olmasından dolayı, maddi destek için tekrar başvuru yaptığında İngiliz hükümetinden yeterli desteği alamamıştır. Bu nedenle Analitik Makine de tasarım olarak kalmış, hayata geçirilememiştir.15
14 Gerard O'Regan, a,g.e., s. 27.
15 Gerard O'Regan, a.g.e., s.44.
Yapımı tamamlanmamış olsa da, Babbage tasarımlarıyla ilgili 1842'de, Torino Üniversitesi'nde bir konferans vermiştir. Sonrasında, bir matematikçi olan Luigi Menabrea (1809-1896), konferansta anlatılanlardan söz eden Fransızca bir makale hazırlamıştır. Babbage bu makaleyi İngilizceye çevirtmek için, sonraları hesapmakineleri tarihinde bir başka dönüm noktası olacak Ada Lovelace’ı (18151852) görevlendirmiştir. Lovelace dokuz ay üzerinde çalıştıktan sonra çevirisini, orijinal belgenin üç katı uzunluğunda bir dizi notla birlikte yayınlamıştır. Çeviriye eklediği notlarda Bernoulli sayılarının, Babbage’ın makinesiyle nasıl hesaplanacağını ayrıntılı olarak anlatmıştır.
Şekil 3. Analitik Makine tasarımı: Soldaki büyük dairesel tekerleklerin etrafında düzenlenmiş yapı, mantıksal ve analitik işlem birimi (CPU) iken, sayfadan sağa doğru uzanan kısım bellektir.
Bilim Müzesi (Londra)16
Babbage, Analitik Makine’de mantıksal ve analitik işlem birimi17, veri depolama birimi (bellek), giriş çıkış üniteleri18 kullanmayı planlamıştır. Ayrıca hesapmakineleri tarihinde ilk defa jakarlı dokuma tezgâhında19 kullanılan delikli kart (punch card) kullanımı örnek alınmıştır. Böylelikle delikli kartlarla girilen komutlar ileherhangi bir aritmetik işlemin makine tarafından yapılabilmesi öngörülmüştür. Burada delikli kart vurgusunun önemi makine ile insan etkileşimini sağlayan bir arabirim olarak iş görmesiyle ilgilidir. Delikli kartlar ilk defa insanın makineye çeşitli komutları verebilmesini sağlamıştır.
16 Computer History Museum (Çevrimiçi), https://www.computerhistory.org/atchm/the-analytical- engine-28-plans-and-counting/, 12 Aralık 2019.
17 Aritmetik işlemler: Toplama, çarpma, çıkarma, bölme. Mantıksal İşlemler: Karşılaştırma, karar verme.
18 Giriş/Çıkış Üniteleri: Verilerin kullanıcıdan girdi olarak alınması ve işlenmiş sonuçların yazılı olarak ekran ya da diğer çıkış birimlerinde gösterimi.
19 J. M. Jacquard, Fransa’da 1805’te patentini aldığı bugün jakarlı dokuma tezgâhı olarak bilinen tezgâhta, desen üzerinde hangi renk ipliğin nerede kullanılacağı karttaki deliklerin pozisyonu ile belirlenmekteydi. Ayrıca bkz. W. A. Atherton, From Compass to Computer: History of Electrical and Electronics Engineering, Macmillan International Higher Education, 1984, s. 269.
Babbage’ın Analitik Makine için kullandığı söz konusu tasarım, günümüz bilgisayarlarının çalışma temellerini oluşturur. Bu temeller üzerine çalışan Ada Lovelace, Analitik Makine’de kullanılmak üzere Bernoulli sayılarını hesaplayan bir diyagram hazırlar. Bu diyagram dünyanın yayınlanmış ilk bilgisayar programı olarak nitelenir. Ada Lovelace bununla da kalmaz Analitik Makine’nin, sayıların ötesine geçebileceğini fark eder. Öyle ki çevirisine eklediği notlarında, müzik, söz dizimi veya görüntüler gibi sayılara dönüştürülebilecek herhangi bir şeyin bilgisayar algoritmaları tarafından manipüle edilebileceğini öne sürer.
1.1.2.1 Makale ve Ada Lovelace’ın Notları
Charles Babbage Tarafından İcat Edilen Analitik Makinenin Kısa Tarifi20
Menabrea’nın makalesinde, Fark Makinesi’nin nasıl çalıştığı hakkında kısa bir bilgilendirme yapılmış ve ardından Analitik Makine’nin nasıl Fark Makinesi’nden daha üstün bir makine olabileceği anlatılmıştır. Menabrea, Analitik Makine’nin basit bir lineer denklem sistemini nasıl çözebileceğini ve iki binom ifadenin bu makine ilenasıl genişletilebileceğini gösteren, makinenin yeteneklerine dair, örnekler vermiştir. Lovelace, bu örneklere ek olarak Not A’da, Analitik Makine’nin Bernoulli Sayılarını nasıl hesaplayacağını anlatan bir diyagram hazırlamıştır.
Makinenin tasarım süreçlerinde Babbage saplantılı olarak sadece sayılarla ilgilenmiştir, Analitik Makine ile sayılar dışında işlem yapılabileceğini düşündüğünü gösteren herhangi bir belge bulunmamaktadır. Ada Lovelace bu noktada notlarında,Analitik Makine ile ilgili Babbage’ın düşünmediği yepyeni bir şey söylemiştir; böyle bir makinenin sadece sayılarla sınırlı olmadığını, eğer makineye müziği sayısal olarak gösterebilirsek müzik de besteleyebileceğinden bahsetmiştir. Analitik makinenin harfler ve sembollerle, sayıları birlikte ele alması için diyagramların nasıl oluşturulabileceğini açıklamıştır. Ayrıca, Analitik Makine’nin, bilgisayar programlarının bugün kullandığı ve döngü (loop) olarak bilinen, bir işlem dizisini tekrar etmesi için bir yöntem teorisi geliştirmiştir. 21
20 L. F. Menabrea, Sketch of The Analytical Engine Invented by Charles Babbage, Çev. Ada Lovelace, 1842. (Çevrimiçi) http://www.fourmilab.ch/babbage/sketch.html#NoteG, 12 Aralık 2019.
21 A.e., s.2.
Ada’nın, Bernoulli sayılarının Analitik Makine ile nasıl hesaplanabileceğini gösteren diyagramını daha iyi anlayabilmek için öncelikle Bernoulli sayılarının ne olduğunu inceleyebiliriz.
1.1.2.2 Kuvvetler Toplamı ve Bernoulli Sayıları
1’den n’ye kadar olan doğal sayıların k’ıncı kuvvetlerinin toplamı eski çağlardan beri matematikçileri meşgul etmiştir.22
İngiliz matematikçi Thomas Hariot (1560-1621), dördüncü kuvvetlere kadar olan toplamları veren simgesel bir formül bulan ilk matematikçi olmuştur. 1631’de, Alman Johann Faulhaber (1580-1635) Academia Algebra adlı kitabında toplamları 17’nci kuvvete kadar hesaplamıştır. İsviçreli matematikçi Jacob Bernoulli (1654- 1705), sabit bir B0, B1, B2, B3, ... dizisi kullanılarak kuvvetlerin toplamını tek seferdeveren bir formül bulan ilk matematikçi olmuştur.
Formülü oluşturmak için Pascal Üçgeni’ni23 kullanan Bernoulli, bu polinomlarıntahmin edilebilir bir model izlediğini fark etmiştir. Bernoulli tarafından Pascal Üçgeni kullanılarak formüllerin üçüncü kuvvete kadar düzenlenmiş hali şu şekildedir:
Bernoulli’nin keşfi, herhangi bir üs için n’ye kadar olan tamsayıların toplamını hesaplamanın önemsiz olduğu anlamına gelmemektedir. Bu yöntemle de belirli bir kuvvete yükseltilen n’ye kadar tüm pozitif tamsayıların toplamını hesaplamak için, belirlenen kuvvete kadar her Bernoulli sayısını bilmek gerekir. Çünkü her Bernoulli sayısı, yalnızca önceki Bernoulli sayıları biliniyorsa hesaplanabilir. Ancak uzun bir Bernoulli sayıları dizisi hesaplamak, her bir güç formülü toplamını elde etmekten çok daha kolaydır, bu nedenle Bernoulli’nin keşfi matematik için büyük bir ilerleme olmuştur.
Bernoulli bir mektubunda “Bu cetvel (yani Bk dizisi) sayesinde, 1000’e kadar olan sayıların onuncu kuvvetlerinin toplamının 1.409.924.241.424.243.424.241.924.242.500 olduğunu bulmak bir çeyrek saatin yarısından daha az zamanımı aldı,” diye yazmıştır. 24
22 Bu konuda çalışan öncü matematikçilerden bazıları; Pisagor (MÖ 572-497), Arşimet (MÖ 287-212),Hintli Aryabhata (doğumu 476), İranlı Ebubekir el Karacı (doğumu 1019), Mısırlı Al Haytam’dır (965- 1039).
23 Adını Fransız matematikçi Blaise Pascal‘dan alan binom katsayılarını içeren üçgene benzeyen yapısından ötürü bu adla anılan bir matematiksel sayı dizisidir. Pascal üçgeninde öncelikle tepeye 1 yazılır. Her satır 1 ile başlayıp 1 ile son bulmalıdır. Örüntü üstteki iki sayının toplamının alta yazılması şeklinde devam eder.
25 Ada Augusta Lovelace, Sketch of The Analytical Engine Invented by Charles Babbage By L. F. MENABREA of Turin, Officer of the Military Engineers from the Bibliothèque Universelle de Genève,October, 1842, No. 82 With notes upon the Memoir by the Translator Ada Augusta, Countess OfLovelace (Çevrimiçi) http://www.fourmilab.ch/babbage/sketch.html#NoteG, 12 Aralık 2019.
Makalenin devamında Lovelace, etkileyici özellikleri olsa da, Analitik Makine'nin gerçekten (insanlar gibi) düşünebileceğinin söylenemeyeceğini savunur. Not G'nin bu bölümü, Alan Turing'in daha sonra “Hesaplama Makineleri ve Zekâ” isimli makalesinde bilgisayarların düşünmesiyle ilgili itirazlar bölümünde “Leydi Lovelace'ın İtirazı” olarak bahsedeceği kısımdır. Çalışmamızın ileriki bölümlerinde bu konuya daha ayrıntılı bakacağımızı söyleyerek devam edelim. Düşünebildiği söylenemese de Lovelace, Analitik Makine’nin olağan üstü şeyler yapabileceğinden söz ederek devam eder. Daha karmaşık problemlerle başa çıkma yeteneğini göstermek için Lovelace, yukarıda bahsettiğimiz Bernoulli sayılarını hesaplayan programını sunar.
Böylelikle Lovelace programıyla, belli ve sonlu sayıda adımdan oluşan yöntem kullanılarak Analitik Makine’nin Bernoulli sayı dizisini nasıl hesaplayabileceğini gösterir. Lovelace’ın yöntemi bilgisayarlar tarihinde bir makine üzerinde çalıştırılabilen ilk bilgisayar programı olarak kabul edilir.26
26 Ada Lovelace’ın yazmış olduğu bu algoritmayı günümüzde en popüler programlama dili olarak bilinen Python ile yazılmış bir örneği için bkz. (Çevrimiçi) Anlatım için https://enigmaticcode.wordpress.com/tag/bernoulli-numbers/ programın kodları için
https://github.com/enigmatic-code/py-analytical_engine, 12 Aralık 2019.
https://github.com/enigmatic-code/py-analytical_engine, 12 Aralık 2019.
1.3 Modern Bilgisayarlar
İngiliz matematikçi ve filozof George Boole (1815-1864), Leibniz’in hayâl ettiği düşünce dilinin matematiksel gösteriminin oluşabilmesi sürecine en önemli katkıyı sağlayan bilim insanıdır. George Boole’dan önce, mantık ve matematik disiplinleri 2000 yıldan uzun bir süredir ayrı ayrı gelişmiştir. O zamana kadar mantık doğal dille yapılmıştır. Oysaki matematik o zamanlarda da doğal dil gibi çifte anlamlılık, belirsizlik vs. gibi sorunları olmayan sıkı kurallara bağlı sembolik bir dil ile yapılmaktaydı. George Boole, şimdi Boole cebiri denilen kavramla, mantık ve matematiğin nasıl birlikte kullanılabildiğini göstermiştir.27
27 Ivor Grattan - Gerard Bornet, George Boole: Selected Manuscripts on Logic and its Philosophy, Springer Basel AG, 1997, s. 30.
Boole cebiri, önermeler ya da nesneler arasındaki bağlantıları tarif edebilen matematiksel bir mantık sistemi olarak tanımlanabilir. Bu mantık sistemi aynı zamanda, günümüzde kullanılan sayısal bilgisayar devreleri tasarımının matematiksel temelini oluşturur, bu nedenle de Boole bilgisayar bilimleri alanınınn kurucusu olarak görülmektedir.
1.3.1 Boole Cebiri
George Boole, Boole cebiri ile mantığın klasik sonuçlarını yeniden üretebilecekbir dizi matematiksel aksiyom bulmak amacındaydı. Böylece başlangıç noktası, x ve y gibi değişkenlerle sıradan cebir, toplama ve çarpma gibi işlemler yapmaktı. Boole’dan önce cebirsel denklemlerdeki harfler sadece sayıları ve geometrik kavramları ifade ediyordu. Boole’un sistematiğiyle ilk defa, küme şeklinde ifade edilebilecek her kavram, sayı kavramında olduğu gibi, harflerle temsil edilmeye vebunlar üzerinde cebirsel işlemler yapılmaya başlandı.
Boole’un böyle bir sistematiği nasıl bir akılyürütme üzerinden kurduğunu daha iyi anlayabilmek için bir örnek üzerinden ilerleyebiliriz.
Örneğin “sarı civciv” öbeğini ele aldığımızda bu kelime öbeğinin anlamını, onu oluşturan iki kelimenin anlamlarını bir araya getirerek yani bu iki kelimeye bir tür işlem uygulayarak oluşturuyoruz/algılıyoruz. Boole burada görülen “sarı”kelimesinin sarı olan her şeyi kapsadığını ve sarı olmayan hiçbir şeyi kapsamadığını, “civciv” kelimesinin ise bütün civcivler topluluğuna karşılık geldiğini düşünmüştü. Buiki kelimeyi cebirsel olarak baş harfleriyle ifade edip cebirsel bir işleme aldığımızda-örneğin çarpma işlemi- sembolik olarak şu şekilde gösterebiliriz: “s.c”. Bu işlem ile “bütün sarı civcivler topluluğu” anlamını elde edebiliriz, sonuç olarak “sarı” ve “civciv” ifadelerinin karşılığı olan iki topluluğun kesişimi sağlanmış olur.
Boole bu işlem ile yapılmış olan şeyi araştırırken önemli bir soru sormuştur: Aynı şeyi kendi kendisiyle bu işleme tabi tutarsak nasıl bir sonuç elde ederiz? “sarı x sarı” veya “civciv x civciv” ne demektir? Bu durumlarda anlamın aynı kaldığını düşünerek Boole şu sonuca varmıştır: Herhangi bir x kavramı için, x.x=x’tir.
Boole bu noktada çok önemli olan bir soru daha sormuştur: Sayılar arasındaki çarpmada x.x=x eşitliğini doğrulayan x değerleri hangi sayılar olabilir?
Cevap 0 ve 1’dir.
Boole böylece yeni bir sonuca daha varmıştır: Öyle ise mantığı cebir dilinde yazarken sadece 0 ve 1 kullanabiliriz.
İki kelime arasında yaptığımız işlemi iki kümenin kesişimi olarak düşünebildiğimize göre; 0, hangi küme olduğundan bağımsız olarak kesiştiğinde içeriği değişmeyen bir küme olmalıdır. Bu şekilde tanımlı olarak bildiğimiz şey ‘boş küme’dir. Aynı şekilde 1 sayısını düşündüğümüzde her şeyi içeren bir küme olmalı düşüncesinden evrensel küme olarak bildiğimiz kümeye ulaşabiliriz.
Böylelikle Boole bir önermenin doğru olduğu anlar kümesi boşsa “yanlış” değilse de “doğru” olarak nitelendirilebileceğinden yola çıkarak “doğru” ve “yanlış” kavramlarını 0 ve 1 ile gösterebileceğimizi ortaya koymuştur.28
Bertrand Russel’ın dediği gibi: “Boole bu çalışmasıyla kuramsal matematiğin yaratıcısı oldu.”29
Boole’un çalışmalarının hayata geçmesi, Claude Elwood Shannon (1916-2001) adında bir öğrencinin lisansüstü tezinde Boole cebirinin, röle anahtarları ve elektrik devrelerinde nasıl işlevsel olabileceğini anlatmasıyla ilerlemiştir.30 Sonrasında düşünme dilinin matematiksel gösterimi fikrinin gelişimininpratik/uygulamada/teknik sonucu olarak elektronik devreler, insanlar ve makinelerarasındaki dilin oluşturulabilmesi için kullanılmıştır.
28 Cem Say, 50 Soruda Yapay Zekâ, Bilim ve Gelecek Kitaplığı, 2018, s.18-20.
29 Daniel J. Cohen, Equations from God: Pure Mathematics and Victorian Faith (Johns Hopkins Studies in the History of Mathematics), The Johns Hopkins University Press, 2007, s.77.
30 Lisans diplomasını Michigan Üniversitesi’nde matematik ve elektrik mühendisliği konularında çiftana dal yaparak alan Claude Elwood Shannon, Boole cebirini lisans eğitimi sırasında aldığı felsefe dersinde öğrenmiştir. “Röle ve Anahtar Devrelerinin Sembolik bir Analizi” (A Symbolic Analysis of Relay and Switching Circuits ) adlı tezi 1938 yılında basıldığında çok dikkat çekmiştir. Bu tez bir sonraki yıl Amerikan Mühendisleri Enstitüsü Alfred Nobel Ödülü’nü almıştır. Ayrıca bkz. Aydın Bodur,Shannon'a Saygı, Elektrik Mühendisleri Odası, 2010.
1.4 Hilbert ve Matematik Dünyası
Geçtiğimiz yüzyılda neyin doğru olup neyin yanlış olduğu, matematiğin nasıl yapılması gerektiği, matematikte geçerli bir ispatın tanımının nasıl yapılabileceği gibi konular matematik dünyasında uzun süre ciddi tartışmalara sebep olmuştur. Bu tartışmaların başlangıç noktası Georg Cantor’un (1845-1918) sonsuz kümeler kuramı olarak bilinir. Cantor bu kuramla küme ve sonsuzluk kavramlarının önemine ve içerdikleri paradokslara dikkat çeken ilk matematikçidir. Cantor’un bu çalışmalarından önce sonsuzluk bir nicelik olarak matematikte yer almıyordu daha çok teolojiye ait bir kavram olarak biliniyordu. Cantor ise sonsuzluklar arasında karşılaştırmalar yapmış, doğal sayıların sayılamaz çoklukta olmalarına karşın reel sayılardan daha az sayıda olduğunu çok zekice bir argüman kullanarak göstermiştir.
1901 yılına gelindiğinde ise Bertrand Russell (1872-1970), önce Cantor’unsonsuz kümeler kuramında ardından mantığın kendisinde bazı paradokslar keşfetmiştir. Buna göre önermeler doğru gözükürken aynı zamanda çelişki oluşturmaktadırlar. Bu duruma örnek olarak Russell kendi kendisinin elemanı olmayan bütün kümelerin kümesi ile ilgili “Bu küme, kendisinin bir elemanı mıdır yoksa değil midir?” sorusunu sorar. Buna göre eğer bu küme kendisinin bir elemanı ise, kendisinin elemanı olmamalıdır. Ve eğer kendisinin elemanı değil ise kendisinin elemanı olmalıdır. Aslında, Russell paradoksu olarak bilinen bu paradoks, “Bu cümle yanlıştır” diyen Epimenides paradoksunun küme kuramcı bir türevidir.
1915’te ise David Hilbert’in, Einstein ile Göttingen Üniversitesi’nde yaptığı çalışmalar neticesinde Genel Görelilik Teorisi ortaya çıkmıştır.31 Hilbert, bu çalışmalar sürecinde de sadece genel görelilik teorisini değil herhangi bir fizik teorisini ispatlamayı sağlamak için gerekli olan minimum aksiyom grubunu belirlemeye çalışmaktaydı. Çünkü Hilbert, matematiğin her türlü soruya cevap bulabileceğine inanıyordu ve aksiyomatik metotla herhangi bir matematiksel problemi çözmek için gerekli araçları belirlemeyi hedefliyordu.32 Bu hedef doğrultusunda Hilbert, Cantor’un sonsuz kümeler kuramı ve Russell paradokslarının matematikte ortaya çıkardığı sarsılmaya çözüm olarak, biçimciliği önermişti. Yani Hilbert’e göre sembolik mantık ile yapay bir dil oluşturulup, içeriğindeki her şey (temel kavramlar, tanımlar, dilbilgisi-gramer vs.) çok net bir şekilde yerleştirildiğinde bütün çelişkilerden kurtulup matematiğin nasıl yapılacağı konusunda evrensel bir kabul oluşturulabilirdi. Bu aksiyomatik sistem sayesinde de paradoksların ortaya çıkması engellenebilir ve matematikteki her şeyin mutlak kesinliği ispatlanabilirdi.
31 Joseph Kouneiher, Foundations of Mathematics and Physics One Century After Hilbert: New Perspective, Springer, 2018, s. 101.
32 Jagdish Mehra, Einstein, Hilbert, And The Theory Of Gravitation, D.Reidel Publishing Company, 1974, s.16-20.
Hilbert’in düşüncesi özetle şunu söylemektedir; eğer matematik nesnelse ve öznel elemanlar barındırmıyorsa ve matematiksel bir ispat “doğru” ya da “yanlış” olarak nitelendiriliyorsa, bu durumda bu doğru ya da yanlış niteliğini belirlemek için kesin kurallar olmalı ve bütün detaylar biliniyor ise bu nitelik yoruma bağlı olmamalıdır. Mutlak doğru ya da yanlış çıkarımını yapan bu sistem sayesinde matematiksel bir ispat otomatik olarak kontrol edilebilecek ve bu sayede matematiksel gerçeklik evrensel olarak kabul edilebilecekti.
Hilbert’in aradığı keskinlikte matematik yapma fikri, Antik Yunan ve Euclid geometrisine kadar uzanır. Fakat Hilbert onlardan farklı olarak böyle bir sistemde sembolik mantığın da kullanılması gerektiğini söylemiştir. Aynı zamanda Hilbert’in bu belirsizlikten kurtulma arayışı sembolik mantığın kurucularından olan Leibniz’in evrensel dil (characteristica universalis) anlayışı ile de benzerlik taşıyordu. Leibniz evrensel dil sayesinde olabilecek tüm tartışmalarda (din, siyaset, günlük hayat vs.) “calculemus”(haydi hesaplayalım) dendiğinde tartışmaya gerek kalmadan kimin doğru kimin yanlış olduğunu görebileceğimiz bir sistem hayal etmişti ve bu sistemle akıl yürütmenin cebir sayesinde netliğe ulaşmasının mümkün olabileceğini düşünmüştü. Leibniz ve Hilbert’e göre objektif matematiksel gerçekliği elde etmenin evrensel ön koşulu; durumu tümüyle hesaplamaya indirgemekti.
1931’de Kurt Gödel (1906-1978) “On Formally Undecidable Propositions in Principia Mathematica and Related Systems” adlı makalesini yayınlamıştı. Gödel bu çalışmasında Hilbert’in düşüncesindeki gibi bir matematik sisteminin asla kurulamayacağını ispatlamıştı. Daha net bir şekilde ifade edersek, bu aksiyomatik sistem ya tutarsız olacak ya da eksik olacaktır aynı anda tam ve tutarlı olamayacaktır.
Gödel bu ispatı ile “ben ispatlanamam” diyen matematiksel ifadeyi yazmayı başarmıştır, bu ispat karmaşık bir yapıdadır ve çok sayıda teknik detay içerir. Aynı zamanda bu ispat fazlaca tekrarlayan fonksiyonlar barındırır ve bu fonksiyonlar listeler üzerinde çalışmaktadır ki bu listeler ve tekrarlanan fonksiyonlar LISP33 programlama dilindeki kullanımla tamamen aynıdır. Yani 1931’de programlama dilleri henüz ortada yokken, Gödel’in makalesinde açıkça bir programlama dili görülür.34
33 LISP(Locator/Identifier Separation Protocol) ilk fonksiyonel programlama dilidir. 1958 yılında yapay zeka(artificial intellingence) teriminin yaratıcısı olan John McCarthy tarafından yapay zeka uygulamalarında kullanılmakla birlikte birçok probleme etkin çözümler bulabilmek için geliştirilmiştir.
34 Gregory J. Chaitin, Thinking about Godel and Turing: Essays on complexity, 1970-2007,World Scientific Publishing Company, 2007, s.110.
1.4.1 Claude Shannon Röle ve Anahtar Devreleri
Claude Shannon lisansüstü tezi için yaptığı araştırmalar sırasında analog35 bir bilgisayar kullanmıştır. Bu bilgisayarın donanım ayarlarını yaparken bu işlemleri elektrikli anahtarlarla yapmanın daha kolay olabileceğini düşünmüştür. Boole cebirinin de bu elektrik anahtarlarını düzenlemekte işlevsel olabileceğini farketmiştir. Shannon’un bu konudaki çalışmaları lisansüstü tezini oluşturmuştur.36
Shannon, Bell Laboratuvarları’ndaki37 çalışma sürecinde şirketin telefonlayapılan aramalarda arayanları otomatik olarak aradıkları kişiye bağlayan röle veanahtar dizilimli sisteminin bir iletişim ağından daha fazlası olabileceğini düşünmüştü ve bu sistemi, büyük bir bilgisayar ağı olarak görmüştür. Shannon’agöre sistem ve otomatik anahtar mekanizmaları; çok karmaşık bir makinenin güzel bir örneğiydi. Bu, pek çok yönden insanın yapmaya çalıştığı en karmaşık makineydi ve yine pek çok yönden de en güvenilir olanıydı.
35 Analog bilgisayarlar sürekli değişen verileri (continuously varying data) işlemek için kullanılan bilgisayarlardır. Değişken veri akışına analog veri adı verilir. Analog bilgisayar, elektrik akımını ölçmek, kapasitörün frekansını ve direncini ölçmek gibi bilimsel ve endüstriyel uygulamalarda kullanılır. Ayrıcabkz. D. E. Hyndman and N. Hiller, Analog and Hybrid Computing, Pergamon Press, 1970.
36 Craig P. Bauer, Secret History The Story of Cryptology, Chapman and Hall / CRC, 2013, s. 108.
37 AT & T’nin resmi Ar-Ge bölümü olan Bell Telefon Laboratuvarları’nın (Bell Labs) kuruluşunun sebebi, ‘Bell System’ çatısı altında yer alan şirketlere yani ABD’de telefon sektöründe hizmet sağlayıcı şirketlere ve bu şirketler için cihaz üreten firmalara tasarım, bakım ve danışmanlık desteği vermektir. Ayrıca bkz. Jon Gertner, The Idea Factory: Bell Labs and the Great Age of American Innovation, Penguin, 2012.
1948 yılında Claude Shannon “İletişimin Matematiksel Teorisi”38 adlı makalesini yayınlar. Bu makalede Shannon, bilginin anlamsal kısmını dışarıda bırakarak bilgiyi olasılık dağılımı ve belirsizlikle ölçmeyi önerdiği bilgi teorisini açıklar.
Enformasyon teorisi olarak da bilinen bilgi teorisinin amacını ortaya çıktığı dönemle değerlendirdiğimizde, 1940’lı yıllarda telekomünikasyona bağlı problemlerin çözümünde bilginin elde edilmesi, aktarılması, işlenmesi ve saklanması konularını incelemek üzere oluşturulmuş olduğunu görüyoruz. Bilgi kavramının modern bilgi teorisine dönüşmesi aşamasında Shannon’un ilgilendiği şey bilgi miktarı olmuştur ve bilgi miktarını temsil etmek için de bir simgeye ihtiyaç duymuştur. Bu noktada George Boole'un sıfır ve birlerden oluşan bitlerini39 kullanmıştır ve daha olası mesajları daha kısa, daha az olası mesajların da daha uzun serilerle kodlanması çıkarımını yapmıştır.40 Böylelikle bu teori, mesajın uzunluğunu olayın oluşma olasılığının ters logaritmasına oranlayarak, bilgisayarlar için entropi41 kavramını oluşturmuştur. Buna göre yeterli sayıda ‘bit’ kullanılarak her türlü bilgi (sayı, harf, ses, görüntü vs.) temsil edilebilecektir. Bilgi teorisi ile iletişim sırasında bozulmaya uğrayabilen enformasyonun, alındığı noktada düzeltilmesi için, hata düzeltici kodların kullanımı da tanımlanmıştır. Günümüzdeki tüm sayısal iletişim teknolojileri; uydu iletişimleri, cep telefonu şebekeleri, internet, Shannon’unenformasyon teorisine dayanarak geliştirilmişlerdir.42
38 C. E. Shannon, “A Mathematical Theory Of Communication”, The Bell System Technical Journal- Nokia Bell Labs, 1948, s. 379-423.
39 Bit kelimesi Binary Digit kelimelerinin birleşiminden oluşur. Sıfır ve bir ikili rakamlarını ifade eder. Günümüz bilgisayarlarındaki en küçük veri boyutu biriminin adıdır. Ayrıca bkz. Eddie Martin, Computer Jargon Dictionary and Thesaurus, Beecroft Publishing, 2006, s.17.
40 Jimmy Soni- Rob Goodman, A Mind at Play: How Claude Shannon Invented the Information Age, Simon and Schuster,2017, s.157.
41 Bir bilgi sisteminin toplam enformasyon potansiyeline, Shannon, o sistemin ‘entropisi’ adını vermişti. Ayrıca bkz. Francisco Escolano Ruiz, Pablo Suau Pérez, Boyán Ivanov Bonev, Information Theory in Computer Vision and Pattern Recognition, Springer-Verlag London, 2009, s. 163.
42 Paul J. Nahin, The Logician and the Engineer: How George Boole and Claude Shannon Created the Information Age, Princeton University Press, 2013, s.115.
İKİNCİ BÖLÜM
MAKİNELER DÜŞÜNEBİLİR Mİ?
Hesap makinelerinden yola çıkılarak gelinen noktada bilgisayarlar, mantıklı davranışlar sergileyen sistemler üretmeyi hedefleyen, yapay zekâ konusuna da farklı bakış açıları kazandırmıştır. Günümüzde teknolojik gelişmeler, "Acaba insanzekâsından daha ileri düzeyde bir yapay zekâya sahip bir sistem üretilebilir mi?" sorusunu sormamıza sebep olmuştur. Ve bu sorunun olumlu bir yanıtı olabileceği fikri doğmuştur.
2.1 Alan Turing (Hesaplama Makineleri ve Zekâ)
Bu alanda gerçekleşen önemli ilerlemelerden biri Alan M. Turing (1912-1954) eliyle sağlanmıştır. Turing, 1950 yılında Mind isimli felsefe dergisinde yayınlanan Hesaplama Makineleri ve Zekâ (Computing Machinery and Intelligence) başlıklı makalesinde daha sonra kültleşecek olan "Makineler düşünebilir mi?" sorusunu sormuştur.
Alan Turing, kendi sorduğu bu soruya cevap verebilmek için öncelikle makine ve düşünme terimlerinin anlamları üzerinde ortak bir karar alınması gerektiğini söyler. “Düşünmek” kavramının tanımlanmasının zorluğundan bahseden Turing, bu tanımı yapmak yerine Taklit Oyunu (Imitation Game) olarak adlandırdığı bir oyun önerir.
Taklit oyunu bir erkek (A), bir kadın (B) ve cinsiyeti önemsiz bir sorgucu (C)arasında oynanır. Sorgucunun amacı diğerlerinden farklı bir odada durarak diğerodadakilere sorduğu sorularla kimin erkek kimin kadın olduğunu tespit etmektir.
Turing’in örnek verdiği şekliyle, sorgucunun A’ya sorduğu sorulardan biri şöyle olabilir: “Bana saçının ne kadar uzun olduğunu söyleyebilir misin?” A’nın oyundaki amacı sorgucuyu kandırıp yanlış karar vermesini sağlamaktır. Bu yüzden şu şekilde cevap verebilir: “Benim saçlarım çok uzun çünkü ben bir kadınım.” Diğer oyuncunun (B) amacıysa sorgucuya yardım etmektir. Kendisi için en iyi strateji şöyle olabilir:“Yalan söylüyor. Kadın olan benim! Asıl benim saçlarım uzun.”1
Eğer bu oyundaki A bir makine olsaydı ne olurdu? Sorgucu erkek ve kadını yanlış tahmin ettiği kadar, makine ve insanı da karıştırır mıydı? Alan Turing makalesinde bu soruların “Makineler düşünebilir mi?” sorusu yerine kullanılabileceğini söylemiştir. Ona göre insanın ya da makinenin birbirlerine karşı olan üstünlükleri bu şekilde göz ardı edilebilecektir.
Turing’e göre taklit oyununda bir makine kendisinin insan olduğuna sorgucuyu ikna edebilirse o makinenin düşünebildiği öne sürülebilir. Fakat Turing makine düşünmesinin insan düşünmesinden farklı olabileceği ile ilgili şöyle bir sorunun sorulabileceğini de göz önünde bulundurur: “Makineler, düşünmek olarak tanımlanabilecek ama insanın yaptığından çok farklı olan bir işlem yapamazlar mı?” Böyle bir olasılığın bulunduğunu fakat böyle bir makine türünün büyük bir etki yaratma olasılığının olmadığını belirtir ve taklit oyunu için en uygun olanın insanın düşünme şekline benzer yapıda olan bir makineyle sağlanabileceğini söyler.2 Böylece Turing makinelerin gerçekleştirdiği işlemlerin insanın düşünme şekline benzer yapıda olmasını, insanların sordukları sorulara insanlardan beklenen şekilde mantıklı cevaplar verebilmelerine indirgemiş aynı zamanda da düşünmek olarak tanımlanabilecek ama insan düşünmesiyle özdeşleşmeyecek işlemler yapmalarının da olası olduğuna değinmiştir. İnsanda düşünme işlemlerinin nasıl gerçekleştiğine dair tüm ayrıntılar henüz bilinmediği için bilgisayarlar ve insanlar düşünme kavramı üzerinden net bir ayrıştırma yapmak hala mümkün değildir.
1 Alan M. Turing, “Computing Machinery and Intelligence”, Mind, 1950, s. 433-460. (Çevrimiçi)https://www.csee.umbc.edu/courses/471/papers/turing.pdf 12 Aralık 2019.
2 A.e. , s.435.
Bununla birlikte Turing taklit oyununda erkek oyuncunun makine taklidi yaparak karşısındakini kendisinin bir makine olduğuna ikna etmesi ihtimalini de çok düşük görmüştür. Böyle bir durumda erkek oyuncunun çok kötü bir gösteri sunacağını, çünkü hesaplama işlemlerinde çok yavaş oluşu ya da hatalı işlem yapışıyla makine olmadığının kısa sürede anlaşılabileceğini düşünür. Yeterince geliştirildiğinde bir makinenin bir insanı taklit edebileceğinden emin olduğu halde bir insanın bir makineyi taklit edebilecek yeteneklere asla sahip olamayacağını makinelerin kusursuz hesap yapma yeteneğini ön plana çıkararak vurgular.
Bu noktada makinelerin insana özgü olan düşünme ile tamamen aynı işlemi yapıyor olmalarının mümkün olmaması aslında tam tersini savunsa da Turing’in söylemlerinden çıkarılabilir. Taklit oyunu ile ilgili bahsettiği insanın makineyi taklit etmeyi denediğinde hata yapmaya makineden daha elverişli bir mekanizmasının olması, düşünce sistemlerinde de farklılıklar olabileceğinin göstergesi sayılabilir. Yanimakineler için insanın düşünme şeklini örnek almak yerine daha kusursuz ve net bir “düşünme” tanımı yapılıp bu tanım makinelere uygulanabilir.
Turing makalesinin “Taklit Oyunuyla Bağlantılı Makineler” (The MachinesConcerned in the Game) başlıklı bölümünde, sorulan sorunun kesinlik kazanması için oyunda geçen makinelerin bir tanımını yapar. Bunun için o dönemde tam olarak tanımlanmamış bir terim olan bugün kullandığımız “bilgisayar” kelimesine çok yakın olarak daha önce kendi tanımladığı evrensel Turing makinesi3 ile eşdeğer olan “sayısal bilgisayar” terimini kullanır. Taklit özellikleri sayesinde çeşitli hesaplama işlemlerini yaparak ayrı ayrı makinelerin tasarımını gereksiz kılmış olmalarından dolayı bu özelliğe sahip makinelerin varlığının öneminden bahseder. Ve bu bölümde son olarak, her durum için uygun bir şekilde programlanmış bir sayısal bilgisayarın tüm işlemleri yapabileceğini net bir şekilde ifade eder.4
3 Evrensel Turing makinesi: Alan Turing tarafından tasarlanmış hayali bir makinedir. Turing'in bu makineyi tasarlamaktaki amacı 'algoritma' olarak tanımlanabilecek her türlü mantıksal işlem bütününü mekanik süreçlere indirgeyebilmektir. Ayrıca bkz. A. A. Puntambekar, Theory Of Computation, Technical Publications, 2009, s. 42.
4 Alan Turing, “On computable numbers, with an application to the Entscheidungsproblem”, Proceedings of the London Mathematical Society, Seri 2, 42 (1936-7), s.230-265.
Makalesini yazmış olduğu dönemde makinelerin bellek kapasitesi ve işlem gücünün Taklit Oyunu’nu geçebilmek için yeterli olmadığını düşünen Turing, gelecek 50 yıl içinde bu yeterliliğe sahip bir makinenin üretilebileceğini ifade etmiştir:
“50 yıl içinde bilgisayarların depolama kapasitelerinin 109 civarında olacağını düşünüyorum. Bu sayede Taklit Oyunu’nu o kadar iyi oynayacaklar ki, yalnızca 5 dakika inceleme yapmasına izin verilen bir sorgucunun verdiği kararların %30'unun yanlış olacağına inanıyorum.”5
Burada görüldüğü gibi sorusuna net bir şekilde cevap vermez sadece oransal olarak bir tahminde bulunur. Bu soruya verilecek olan “Evet” ya da “Hayır” cevabının henüz net olmayışı aradaki sınırın belirsizliğini ve bu sorunun tartışmaya açık olduğunu da göstermektedir.
Günümüzde birçok bilim insanı, geliştirilmiş ve güncellenmiş bir Turing Testi'nin gerektiğini iddia etmektedir.6 Turing Testi’nde bilgisayarların insan düşünüşünü taklit edip edemediklerini anlamak için bilgisayarlara sorular sorup, onların sorulan bu sorulara insanlar gibi yavaş cevap vermesi, klavye hataları yapması, duygusal tepkiler vermesi ya da bazen rastgele aklına gelmiş gibi konuyla ilgisiz şeyler söylemesi onlar için avantaj sağlamaktadır. Fakat güçlü yapay zekânın insanlar gibi hata yapması beklenmez, dolayısıyla onun insanlar gibi hatalar yapmasının işe yaradığı bir teste girmesi hedeflenen başarı açısından faydalı olmadığı için Turing Testi’nin güncellenmesi ve bu güncelleme ile sorulan “Bilgisayarlar düşünebilir mi?” sorusunun da değiştirilerek “Bilgisayarlar bilinç sahibi midir?” şeklini alması daha uygun olabilir. Çünkü Turing’in verdiği örnekten de anlaşıldığı gibi bu testte bilgisayar için amaç sorgucuyu insan olduğuna ikna etmektir. Fakat günümüzde hedeflenen, bilgisayarların insanlar gibi düşünmesi değil insanın çözemediği problemlere yanıtlar bulabilmesidir. İnsanların çözemediği problemler için doğru çözüm yöntemini bulmanın yolu ise insanlar gibi düşünmemekten geçiyor olabilir.
5 Alan M. Turing, “Computing Machinery and Intelligence”, s.441.
6 J. Copeland, J. Bowen, M. Sprevak, R. Wilson, The Turing Guide, Oxford University Press, 2017, s.272.
Turing düşünmenin ne olduğunun açıklanmasının zorluğunu, bilgisayarların düşünmesini sağlayarak açıklayabileceğimizi ve taklit oyunu gibi varsayımların yararlı araştırma yolları önerdiğini belirtir. Son bölümde ise "Makineler düşünebilir mi?" sorusu olumlu yanıtlandığında farklı görüşlerin ortaya çıkabileceğini göz önünde bulundurur. Bu farklı görüşleri de dinlemek zorunda olduğunu ifade ederek, makinelerin düşünemeyeceği yönündeki iddiaları değerlendirir.
2.1.1 Teolojik İtirazlar
Söz konusu iddialardan biri; teolojik itiraz olarak bilinen, düşünmenin insan türüne özgü bir yetenek olduğunu savunan, diğer hayvan ve makinelerin düşünemeyeceğini söyleyen teistik görüştür. Buna göre yaratıcı, tüm insanlara ölümsüz birer ruh vermiştir ve düşüncenin temel kaynağı da bu ruhtur. Turing bu itirazı kesin bir dille reddederken teolojik terimler kullanır, bu iddianın Tanrı’nın gücü üzerine ciddi bir kısıtlama getirdiğini belirtir. Eğer uygun görürse Tanrı’nın bir file ruh verme özgürlüğüne sahip olduğuna da inanılması gerektiğini vurgular. Böylelikle, eğer her şeyi yaratan bir tanrı varsa, biyolojik yolla doğmuş olan bir çocuğu onun yaratması gibi, bizim doğru şartlarda bir makineyi bir araya getirmemizdeki bütünlüğü de yaratmış olabileceğini ifade eder.7 Son olarak kendisinin teolojik tartışmalardan etkilenmediğini belirtir ve Galileo döneminde Kopernik kuramlarının İncil’den alıntılarla çürütülmüş olduğunu örnek verir, bilimsel anlamda yaşanan ilerlemeler sayesinde, makalenin yazılmış olduğu çağda bu tür bir tartışmanın olamayacağını düşündüğünü de ekler.
7 Alan M. Turing, “Computing Machinery and Intelligence”, s.442.
2.1.2 Kafaları Kuma Gömme İtirazı
Diğer bir itiraz, Turing’in “kafaları kuma gömme itirazı” olarak adlandırdığı itirazdır. Makalede şu şekilde ifade edilmiştir: "Makinelerin düşünmesinin sonucu çok korkunç olabilir. Düşünemeyeceklerini umalım ve buna inanalım."8 Bu ifade Turing’e göre insanların makinelerin gücünü görmezden gelerek kendilerinde olan yönetme idare etme gibi özellikleri makinelere vermek istememelerinden ileri gelen vedüşünmeyi dolayısıyla da insanı yücelten bir itirazdır. Turing bu itirazı aydınların, düşünme eyleminin; sadece kendilerine özgü olmasını istemeleri sebebiyle, kendilerini rahatlatmak için yaptıkları bir itiraz olarak görür ve eleştirir. Bu argümanı çürütmeye değer bulmaz ve bu şekilde düşünen kişilerin teselli edilmesini dahauygun bulduğunu ekler.
8 Alan M. Turing, a.y. , s. 442.
2.1.3 Matematiksel İtirazlar
Matematiksel açıdan yapılan itirazlarda, Gödel’in (1906-1978) Tamamlanamazlık Teoremi9 (Incompleteness Theorem) uyarınca mantık temelli bir makinenin cevaplayabileceği soru sayısının kısıtlı olduğu savunulur. Gödel’in Tamamlanamazlık Teoremi; o dönemin matematikçilerine yeni matematiksel teoremler üretebilen makinelerin inşası yolunda mantıksal engeller olabileceğini düşündürmüştür.
9 1928’de David Hilbert(1862-1943) ve Wilhelm Ackermann(1896-1962), matematikçilere, yeterince geliştirilmiş olan biçimsel dille yazılmış herhangi bir mantıksal önermenin verilen öncüller kullanılarak kanıtlanabilir olup olmadığını saptayabilen bir yöntemin (günümüzde kullandığımız terimle, biralgoritmanın) bulunması için çağrıda bulundular. Böyle bir algoritmanın var olduğunu düşünüyorlardı bu algoritma keşfedildiğinde artık matematikçiler ispat işlerini bu algoritmaya göre çalışan makinelere bırakabilir, ilgilendikleri herhangi bir önermenin doğru mu yanlış mı olduğunu otomatikolarak öğrenebilirlerdi.
Fakat Gödel bunun olanaksızlığını gösterdi. Bunu kısaca şu şekilde yaptı: ‘Bu önerme ispatlanamaz’ifadesini (G) aritmetik sisteminde formüle etti. Aynı şekilde G ifadesinin değili ola ‘bu önerme ispatlanabilir’ ifadesini de formüle etti. Daha sonra, G ifadesinin aritmetik olarak doğruluğu hesaplanabilirse, G ifadesinin değilinin de doğruluğunun hesaplanabileceğini gösterdi.
Ve Gödel buradan şu iki sonuca vardı:
1.Temel aritmetik içeren aksiyomatik bir sistem tutarlı ise eksiksiz değildir.
2.Temel aritmetik içeren aksiyomatik bir sistemin tutarlılığını sistemin kendi içinden (sistemin kendi formüllerini ve işlemlerini kullanarak) ispatlamak mümkün değildir.
G ifadesi sistemin içine bir aksiyom olarak yerleştirilse bile, yeni bir Gödel cümlesi çıkartılabilir. Yani ne kadar aksiyom eklersek ekleyelim, böyle bir sistemde doğruluğu ya da yanlışlığı ispatlanamayacak bir Gödel cümlesi bulunacaktır.
Ayrıca bkz. Joan Roselló, Hilbert, Göttingen and the Development of Modern Mathematics,Cambridge Scholars Publishing, 2019, s. 193.
Aslında burada merak edilen şey: Tamamlanamazlık Teoremi sayesinde anladığımız üzere, tamamlayamadığımız formel bir bilgi ile nasıl tamamlanmış bir zeka inşa edileceğidir. Veya matematiksel önermeler formel olduğu halde bunlar hakkında bile bir karar verici inşa edemezken, insan zekasını nasıl formelleştirip makineye sığdırılacağı sorunsalıdır.
Turing de 28 Mayıs 1936'da sunduğu “Hesaplanabilir Sayılar: Karar Verme Probleminin bir Uygulaması”10 başlıklı makalesinde, Gödel'in 1931'de aritmetik-tabanlı biçimsel dille hazırladığı hesaplama ve kanıtın sınırlarını makineler üzerinde yeniden belirlemiştir. Matematikte önermelerin ispatlanabilir olup olmadığına kararverme problemini, Turing matematikçilerin problemi olmaktan çıkarmış ve bilgisayarların bir problemi olan durma problemine (halting problem)11 indirgemiştir. Bu çalışmasında günümüzde Turing makineleri olarak bildiğimiz ispatı ortaya atmıştır. Bu ispatla eğer bir algoritma ile temsil edilmesi mümkün ise her türlü matematiksel problemin böyle bir çeşit makine kullanılarak çözülebileceğini göstermiştir. Turing bu makalede, bugün "hesaplama" (computation) olarak bildiğimiz olgunun tanımını yapmakla kalmamış, aynı zamanda hesaplamanın başarabileceklerinin sınırlarını da ortaya koymuştur.
Turing’in ispatını daha iyi anlayabilmek için öncelikle yaşadığı dönemde bilgi işlem makinelerini ve işlevlerini inceleyebiliriz. O dönemde "bilgisayar" (computer) sözcüğü, bugün olduğu gibi bir makineye işaret etmek için kullanılan bir kelime değildi. Bilgisayar kelimesi "bilgiyi sayan insan" anlamına gelmekteydi. Çoğunlukla matematiği iyi olan kadınlar arasından seçilen bu bilgiyi sayan insanlar, devletten ya da diğer büyük kurumlardan gelen verileri defterlere ve kâğıtlara kaydeder, gerekli olan hesaplamaları yapar, tüm sonuçları doğru şekilde işlediklerinden emin olurlardı. Sistemler bu şekilde işlemekteydi, önemli ve uzun bir hesaplama işi gerektiğinde, hesaplanması gereken sayılar bu kişilere verilir ve bu "bilgiyi sayan insanlar", uzun süreler çalışarak, yaptıkları hesaplamaların doğru olduğunu testederek sonucu, hesabı isteyen kişilere (devlet yetkililerine, bilim insanlarına, vs.)iletirlerdi.12 Bir önceki bölümde bahsettiğimiz gibi Charles Babbage’ın fark makinesi tasarımı da insanların çok fazla zaman harcayarak bazen hatalı sonuçlara ulaştığı bu işlemleri otomatik olarak yapacak bir makine arayışından doğmuştu. Bu durum Turing’in de dikkatini çekmiştir insanların yapmak zorunda olduğu bu çok basit ama önemli işin, mekanik ya da elektronik adımlarla kolayca makinelere yaptırılabileceğini öngörmüştür. Bu öngörüsü nedeniyle de “Hesaplanabilir Sayılar” isimli makalesi, günümüz bilgisayarlarının temellerini oluşturan bir çalışma olarak bilinmektedir. Bu makaleyi daha detaylı olarak inceleyelim.
10 Alan M. Turing, On Computable Numbers, With An Application To The Entscheidungsproblem, 1936. (Çevrimiçi) http://www.cs.virginia.edu/~robins/Turing_Paper_1936.pdf 12 Aralık 2019.
11 Alan Turing, 1936’da hesaplanabilirlikle ilgili temel bir sorun olan “durma problemi” ortaya koydu. Bu problem, herhangi bir girdiyi işleyen herhangi bir bilgisayar programının önünde sonunda durupdurmayacağını söyleyecek genel bir algoritma olup olmadığını sorar. Alan Turing bir Turingmakinesine herhangi bir girdi verildiğinde makinenin önünde sonunda durup durmayacağını söyleyebilecek genel bir algoritma olmadığını ispatladı. Ayrıca bkz. Chris Bernhardt, Turing's Vision: The Birth of Computer Science, MIT Press, 2016, s. 24.
12 David Alan Grier, When Computers Were Human, Princeton University Press, 2013, s. 138.
2.1.3.1 Makale: Hesaplanabilir Sayılar - Karar Verme Probleminin birUygulaması
Turing makalesine, matematiksel işlemler yapan, yorulma, uyuma, acıkma, yaşlanma, dikkat dağınıklığı, kâğıt/kalem eksikliği gibi problemleri olmayan, birinsanın yerine geçebilecek bir “makine” türünü net bir şekilde tanımlayarak başlar. Buna göre bir Turing makinesi, önceden tanımlanan kuralları uygulayarak tüm matematiksel fonksiyonları hesaplayabilir. Bu hesaplamayı oldukça basit ve mekanik bir yolla yapar. Turing’in açıkladığı bir başka özellik ise evrensel Turing makinesiolarak bilinir, yani öyle bir Turing makinesi vardır ki bu, diğer tüm Turing makinelerinin davranışını taklit edebilir. Böylelikle Turing, Turing makinelerinin her sistemin benzetimini (simülasyon) yapabilme niteliğini, tek bir makineye sonsuz sayıda farklı iş yaptırabilmek için kullanabileceğimizi de keşfetmiştir, günümüz bilgisayar biliminin temel mimari modeli olan yapı da budur.
Aslında Turing makinesi bir bilgisayar modeli olma amacıyla değil, daha önce Gödel’in de üzerinde çalışmış olduğu, Hilbert'in ortaya attığı; "Acaba bütün matematik problemleri için algoritmik bir çözüm var mıdır?" sorusunu cevaplamak amacıyla tasarlanmıştır ve bu makinenin somut bir mekanizması da yoktur.
Makinenin bileşenlerinden anlaşılan, Turing bu makineyi çözmek istediği matematiksel problemin güçlüğü nedeniyle, sonsuz olanak taşıyacak biçimde düzenlemiştir. Örneğin makinenin bir bellek olarak kullandığı, verileri üzerine işleyebileceği sonsuz uzunlukta bir şerit tasarlamıştır. Bunun yanında verileri okuyan ve yazan bir okuma-yazma kafası ve algoritmayı işleten bir karar verme ünitesi bulunur. Okuma-yazma kafası, şerit üzerinde sağa sola hareket edebilir, çıktıları daaynı şerit üzerine işleyebilir. Mekanizmanın en önemli parçası olan karar verme ünitesinin güncel karşılığı ise bir işlemcidir. Bu ünite, bant üzerinde o anda üzerinde bulunduğu karedeki duruma göre bir takım kararlar verir, bu kararlar, kafayı sağaveya sola hareket ettirmek, kareyi değiştirmek veya durmak olabilir. Bu noktada durma kararı, Turing makinesinin doğmasına yol açan problemle ilişkilidir. Bir problemin algoritmik olarak ifade edilip edilemeyeceği Turing makinesinin belirliişlemler sonucunda durması şekline indirgenmiştir. Buradaki durma, başarılı olma anlamına gelmektedir. Makine durduğunda sorulan probleme bir çözüm üretmiş demektir. Fakat bazı problemler için, makinenin ne zaman duracağını bilmek mümkün değildir. Bu noktada ‘durma problemi’ (halting problem) yani Turing makinesinin bir problemin işlemsel olarak bir çözümünün olup olmadığına karar verememesi aynı işlemi sürekli tekrar etmesi ama bir sonuca ulaşamaması problemi ortaya çıkar. Durma probleminin ortaya çıkmasıyla bazı problemlerin algoritmik bir çözümü olmadığı bir kez daha ispatlanmıştır.
Turing bu şekilde kendisinin de katkı sağlamış olduğu matematiksel itirazlara cevap olarak yine de makinelere mantık sistemlerini ve mantık sistemlerine makineleri tanımlamanın yollarını bulmak zorunda olduğumuzu vurgular.
Turing, Gödel’in Tamamlanamazlık Teoremi üzerinden yapılan bu itirazın kolayca göz ardı edilemeyeceğini ifade eder fakat makinelerin gücünün sınırları olduğu saptandığı halde “insan zekâsının benzer kısıtlamaları olmadığının hiçbir kanıt gösterilmeden ileri sürülmesini doğru bulmadığını”13 belirtir. Bununla birlikte son olarak matematiksel argümanın taraftarlarının; taklitçilik oyununu, makinelerin düşünebilmesi tartışmalarının temeli olarak kabul edebileceklerini fakat bundan önceki iki itirazı ileri sürenlerin ise herhalde hiçbir ölçüte ilgi göstermeyeceklerini ekler. Bu ifadelerinden, Turing’in bu konuyu tartışmayı gerekli ve faydalı bulduğunu çıkarabiliriz.
13 Douglas R. Hofstadter- Daniel C. Dennett, Aklın G'özü: Benlik ve Ruh Üzerine Hayaller ve Düşünceler (Çev: Füsun Doruker), Boğaziçi Üniversitesi Yayınevi, 2005, s. 64.
2.1.4 Bilinç Argümanı
Turing makinelerin düşünemeyeceğine ilişkin bir başka karşı çıkış olarak İngiliz Nörolog, Profesör Jefferson’ın (1886-1961) argümanını konu eder. Bu argüman 1949yılında Profesör Geoffrey Jefferson tarafından ortaya atılmıştır, Jefferson bugörüşünü Lister Söylevi'nde ifade etmiştir.14 Turing de, Jefferson’un ifadelerini alıntılayarak makalesinde yer vermiştir:
“Bir makine, yalnızca simgelerin şans eseri dizilmesinin dışında, duygular ve düşünceler nedeniyle bir şiir yazıp ya da bir konçerto bestelemedikçe, bir beyne eşit olduğunu kabul edemeyiz; ayrıca bunu yazdığı gibi yazdığını da bilmesi gerekir. Hiçbir mekanizma (kolay birhile olan yapay bir sinyal dışında) başarısından dolayı keyif duyamaz, şalterleri atınca üzülemez, iltifatlara sevinemez, hatalarından dolayı kederlenemez, cinsellikle baştan çıkarılamaz, istediğini elde edemeyince öfkelenemez.”15
14 Sara Turing, Alan M. Turing: Centenary Edition, Cambridge University Press, 2012, s. 101.
15 Douglas R. Hofstadter- Daniel C. Dennett, a.g.e, s. 65. Ayrıca bkz. G. Jefferson, The Mind of Mechanical Man, Lister Oration for 1949, British Medical Journal, 1949, s.1105-1121.
Burada vurgulanan farkında olma durumu Jefferson tarafından insanlara özgü bir özellik olarak görülür. İnsanlar bunu yapabildiği için türümüzü homo sapiens sapiens16 olarak adlandırıyoruz; yani farkında olduğunun farkında olan insan. Bu da bilincin temel şartının farkındalık olduğunu düşündürüyor. Makine zekâsını insan zekâsı üzerinden tanımlayan Turing’in de insan bilincini makinelerin düşünebilmesinden farklı gördüğünü söyleyebiliriz. Ona göre taklitçilik oyunu için bilincin tanımlanmasına gerek yoktur. Turing bu düşüncelerini şu şekilde ifade etmiştir:
“Bilinçlilik konusunda hiçbir gizem olmadığı izlenimini vermeye çabalamıyorum. Örneğin bilinçliliği saptama girişimlerinde bir çeşit paradoks hep vardır. Yine de bizim makalemizdeki sözü edilen soruyu yanıtlamadan önce bu gizemlerin çözülmesi gerektiğini de düşünmüyorum.”17
16 Homo sapiens sapiens, "düşündüğünün üstüne düşünebilen insan" demektir. Bu tanımı ortaya ilkRene Descartes atmıştır. Günümüz modern insanının bu alt türe mensup olduğu düşünülür. Ancakçoğunlukla sadece Homo sapiens olarak anılır. Ayrıca bkz. Stephen Tomkins, The Origins of Humankind, Cambridge University Press, 1998, s. 107. D. Gambier, Fossil hominids from the early upper Paleolithic (Aurignacian) of France, Mellars & C. Stringer (Eds.), The human revolution, Princeton, NJ: Princeton University Press, 1989,s. 194–211.
17 Alan M. Turing, “Computing Machinery and Intelligence”, s. 443.
Her ne kadar Turing, bilinç sorununa girmeden makineler düşünebilir mi sorusu üzerinden bir tartışma yürütse de Douglas R. Hofstadter’in Turing testi üzerinden işaret ettiği bir bilinç tartışmasından söz edilebilir. Douglas R. Hofstadter bilincin belirgin bir organizasyon modelinden kaynaklandığını ve zamanla bu modelin anlaşılabileceğinden söz eder. Buna göre bilinçlilik, dış evreni belirli bir yolla zihinsel olarak içe yansıtmayı ve zihinsel olarak oluşmuş olan bu iç modeli esas alarak dışsal gerçekliğe yanıt verme yeteneğini gerektirir.18 Burada kullanılan “dış evreni belirli bir yolla zihinsel olarak içe yansıtmak” deyimi bilgisayarların yaptığı gibi etrafımızda gördüğümüz varlıkların davranışlarını düşüncemizle simule etme ve gelecekte ne olacakları ile ilgili akıl yürütme özelliğimizdir. Bu özellik yapay zekâya sahip bilgisayarların yapmasını beklediğimiz işlemlerin temelini oluşturan yapıdır. Ayrıca bu tanıma göre bilinçli bir makine için en önemli özellik ileri düzeyde geliştirilmiş ve her yapıya uyarlanabilecek şekilde esnek bir öz-modeli olmasıdır. Buna göre esnek öz-model bir bilgisayarın kendi kendini programlayabilmesinin de ön koşulu olarak kabul edilebilir.
Jefferson’ın iddiasına göre ise; bir makinenin sadece içindeki sembolleri kullanması önemli değildir. Makine kendi hissettiği duygu ve düşünceleriyle bir söz yazıp ya da bir beste yapana kadar hatta yazdığı söz ve bestesinin farkında oluponunla gurur duyana kadar bilinç sahibidir, diyemeyiz. Ona göre bir makinenin bilinçli olması sadece bir eser üretmesi de değil aynı zamanda başarısızlığına üzülmesi, bir iltifat karşısında sevinmesi, bir şeyi elde edemediğinde sinirlenmesigibi hisler (duygular) barındırıyor olması demektir.
Jefferson, sadece belirli sembollerin bir araya gelmesinin zihni anlatmaya yetmeyeceğini, geçmiş düşünceler ve duygular kullanılarak bestelenen bir müzik ya da yazılmış bir şiir ortaya koymadan bir makinenin insana eş değer görülemeyeceğine işaret eder. Bununla birlikte bir insanın yaşadığı kederi, mutluluğu, cinsel çekimi, öfkeyi ya da depresyonu bir makinenin yaşayamayacağını da ileri sürer.
Turing, Jefferson’ın iddiasını şu biçimde yeniden düzenler: “...bir makinenin düşündüğünden emin olmak için, makinenin kendisi olmamız ve düşündüğümüzü hissetmemiz gerekiyor. (...) yine bir insanın düşündüğünü anlamanın tek yolu da o insan olmaktır”19 Turing, bu görüşü tekbenci bakış açısı olarak değerlendirir. Sonrasında zihin felsefesi tartışmaları açısından öteki zihinler sorunu olarak belirginleşecek bu nokta, herkesin kendi zihnine dolaysız, başkasının zihnine dolaylı erişiminden kaynaklanan gerilimi konu eder. Turing, zihinle ilgili bu gerilimin hem makineler hem de insanlar için aynı düzeyde durduğunu belirterek, Jefferson’ın iddiasından vazgeçmeye ikna edilebileceğini varsayar.
18 Douglas R. Hofstadter- Daniel C. Dennett, a.g.e., s. 85-87.
19 Alan M. Turing, “Computing Machinery and Intelligence”, s. 455.
Tekrar Jefferson’ın söylemine dönersek burada parantez içinde “kolay bir hile”olarak nitelenen ve tüm insani durumların dışında tutulan “yapay sinyal”, makinenin yaptığı şeyin doğru olduğu bilgisini edindiği, kendi sistemi içinde olan onaylanma sinyalidir (makine için ödül mekanizmasıdır). 21.yüzyıl moleküler hücre biyolojisi alanındaki önemli gelişmelere baktığımızda, bilim insanlarının canlılarda bulunan vebeyindeki kimyasal iletime katkısı olan farklı iletim maddelerini (nörotransmitterleri) ve bu maddelerin hangi işlevlerde rol aldığını gözlemlemiş olduklarını görürüz.20 Bu gözlemler sayesinde artık birçok kimyasalın duygusal değişimlerimiz üzerinde etkili olduğu bilinmektedir. Hormonların etkisini çok temel düzeyde inceleyecek olursak, bize iyi hissettiren bir durumun, yani beynimizdeki ödül mekanizmasını tetikleyen davranışlarımızın, ilkel insanların hayatta kalma şansını arttıran unsurlar olduğunu görebiliriz (örneğin hayatta kalmak ve türümüzü devam ettirmek için öncüller; beslenme21, güvenlik, üremek, vb. ). Mutlu olmamızı sağlayan kimyasallar, hem toplumsal iletişim, hem de bireylerin genel sağlığı için olumlu tutum sergilendiğinde ortaya çıkarlar.22 Böylece insanlar olarak bu kimyasalların salgılanmasını arttıracak davranışlara eğilimimiz vardır ve bizde var olan bu ödül mekanizmasının, insan beynini örnek alarak geliştirilen, makineler için de oluşturulması sağlanabilir. Özellikle düşünen ya da otonom bir makine yapmak istiyorsak ona yaptırmak istediğimiz işler üzerinde motive olmasını sağlayacak bir kod parçacığımız (yapay sinyal) olmalıdır.
20 D.G. Hardie, Biochemical Messengers: Hormones, Neurotransmitters and Growth Factors, Springer Science & Business Media, 1991, s. 21.
21 Beynin yemek yemeğe nasıl karar verdiğiyle ilgili bir makale için bkz. (Çevrimiçi) “How Does the Brain Implement Adaptive Decision Making to Eat”, The Journal of Neuroscience, 2015, s.13868- 13878. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4604225/pdf/zns13868.pdf, 12 Aralık 2019.22 22 Joe Herbert, The Minder Brain: How Your Brain Keeps You Alive, Protects You from Danger, and Ensures that You Reproduce, World Scientific, 2007, s. 55-64.
İnsanlığın gelişim süreciyle ilgili Ayrıca bkz. Aynı eser: “Doğal seçilimle genele fayda sağlayan, türe yararlı, hatta vazgeçilmez olan dürtü değiştirilmeksizin bırakılırken, zararlı olabilecek dürtülerin özel durumlarını önlemek için bir sosyal engel mekanizması ortaya çıkar.”
Turing bu noktada Jefferson’un aşırı ve tekbenci bakış açısını kabul etmek istemeyeceğini ve bu konuda taklitçilik oyununu bir sınav olarak kabul edebileceğiniifade eder. Bu görüşe karşı savunmasının son bölümünde daha önce örneklenmiş olan taklitçilik oyununun daha karmaşık bir örnek diyaloguna yer verir ve “Böyle gerçekçi bir diyalog içinde olduğunuzda hâlâ karşınızda bir makine olduğundan şüphe edebilir misiniz?”23 diye de sorar. Burada Turing’in makinelerle ilgili görüşlerinin nelerin mümkün olmadığı üzerine odaklanmak yerine, “nasıl mümkün olabilir” düşüncesine odaklandığını görmekteyiz.
23 Alan M. Turing, “Computing Machinery and Intelligence”, s. 456.
2.1.5 Çeşitli Engeller Argümanı
Beşinci itiraz, çeşitli engeller argümanıdır ve neredeyse bilinçlilik argümanı ile aynı içeriğe sahiptir. Bu argümanda âşık olmak, tat almak, hatalar yapmak gibi farklı yönlerden bilinçli olmanın getirdiği özelliklerden bahsedilir ve makinelerin bueylemleri insanlar gibi gerçekleştiremeyeceği iddia edilir. Turing bu tür argümanlarıyine bilişsel olarak görür. Yani Turing’e göre bu tür insani faaliyetler de temelde biyolojik yapıyla birleşik bilişsel süreçlerdir, bu isteklerle veya korkularla ilgili psikolojik davranışsal süreçler biçimsel olarak uygulanırsa/programlanırsa, makineler de tasarlandığı ölçüde isteyen, korkan, tat alan ve hatalar yapan zihinler olacaktır.
Turing bu argümanı, insanlardaki bilimsel tümevarım üzerine kurulmuş sınırlandırmalar olarak görür. Ona göre insanın yaptıkları ve alışkanlıkları bilimsel tümevarımın uygulanmasına uygun değildir. Bu konuda tümevarım ile güvenilir sonuçlara ulaşmak için uzay ve zamanın önemli derecede büyük bir bölümünün araştırılması ve açıklanabilmesi gerekmektedir. Turing bu eleştirinin ilginç ve sempatik olmadığını söylese de anlamaya çalışan bir yaklaşım sergileyerek aslındane demek istendiğini incelemeye çalışır. Bu iddiayla ilgili tespit ettiği şey; iki çeşit hatanın birbirine karıştırılmasıdır. Bu hatalar işlev hatası ve sonuç hatasıdır. İşlev hataları, mekanik ya da elektriksel bir sorun sebebiyle makinenin tasarlanmış olanın dışında çıktı üretmesidir. Felsefe tartışmalarında bu türden hatalar göz ardı edilmek istendiğinden, tartışma 'soyut makineler' üzerinden devam ettirilir. Burada bahsedilen soyut makineler fiziksel nesneler değil matematiksel kurgulardır ve işlev hatası yapmaları mümkün değildir. Sonuç hataları ise makinenin çıktılarında oluşan beklenmeyen hatalardır. Bu hatalar makinenin sinyallerine bazı anlamlar katıldığı zaman ortaya çıkar. Böyle bir makine bilimsel tümevarımla sonuca ulaşma yöntemine sahip olabilir. Matematik ve mantık da tümdengelim yöntemi ile kesin doğru olarak kabul edilen bilgilerden çıkarımlar yapılarak yeni bilgi üretme yöntemleridir. Turing’e göre böyle bir yöntem doğal olarak bazı durumlarda hatalı sonuçlara ulaşabilir.
Buna göre, makineler çirkindir, sınırlı amaçlar için tasarlanmıştır, biraz farklı bir amaç söz konusu olunca, işe yaramazlar, davranış farklılıklarındaki çeşitlilik çok azdırvs. iddialarını “Bir makinenin davranış çeşitliliğine sahip olmaması onun depolama alanının sınırlarıyla ilgilidir.”24 Diye cevaplayarak çözüme kavuşturur. Çünkü Turing depolama alanı problemlerinin yakın bir gelecekte aşılabileceğini iddia etmiştir. Turing’e göre bu problem aşıldığında makinenin davranış çeşitliliği sınırlarıyla ilgili sıkıntının kaynağı da ortadan kalkmış olacaktır.
24 Alan M. Turing, “Computing Machinery and Intelligence”, s. 447.
2.1.6 Lady Lovelace'ın İtirazı
Lady Lovelace, Charles Babbage’ın tasarımı olan Analitik Makine hakkında yazdığı notlarda makinelerin geleceğiyle ilgili bazı tahminlerde bulunmuştur. Bunlardan biri makinelerin bir şeyi kendiliğinden yapmasının mümkün olmadığı ve komut verdiğimizde bunun kendisinde karşılığı bulunan komutları algılayabildiği yönündedir. Turing bu fikre, Hartree’nin görüşüyle karşı çıkar. Bu görüşe görekendisi ile ilgili düşünebilecek veya yeni şeyler öğrenebilecek bir makine üretmenin mümkün olmadığını şimdiden söyleyerek makinelere sınırlar koymak doğru ve mantıklı değildir. Turing bu görüşe, kendiliğinden bir şey yapma durumunun da programlanabileceğini ekler. Ona göre bir program çok daha fazla parametreyi girdi olarak alırsa, hatta bu girdilere fiziksel rastlantı da eklenirse, bilgisayarlar kendi başlarına bir şeyler yapabileceklerdir.
Turing, Lady Lovelace’ın savına, makalesinin son bölümü olan Öğrenen Makineler (Learning Machines) başlıklı bölümde günümüz makine öğrenmesi kavramına yaklaşan bir tutumla yanıt verir. Çalışmamızda ise bu argüman günümüzteknolojisi ile düşünüldüğünde şöyle yanıtlanabilir:
Bir yazılım, makine öğrenmesi algoritmalarıyla, girilen sonlu sayıdaki veriyiişleyerek o veriler hakkında bir model oluşturur sonrasında bu modeli test eder. Hata durumlarını saptayabilirse kullandığı modele dönüp bu modeli değiştirir böylece ideal modeli geliştirebilir sonrasında da yeni veriler için doğru çıkarımlar yapabilir. Yani makine öğrenmesi gibi modern yazılım teknikleri öngörülenin dışında davranışlar sergileyebilir. Fakat makine öğrenmesi ve buna benzer algoritmalar yine bir programcı tarafından bilgisayara yüklenerek, ona tanıtılarak gerçekleştirilir yani yazılımın kendisi bu metotları uygulamaya karar vermez. Bir makinenin yapabileceklerinin neler olduğunu tüm açıklığıyla ifade etmese de, Lovelace “bir makineye bizim yapmasını istediğimiz her şeyi yaptırabiliriz” derken, aslında bir sınır koymuş değildi. Turing’in de alıntılayarak yer verdiği gibi Lovelace’ın ifadesi şu şekildeydi:
“Analitik Makine herhangi bir şeyi kendiliğinden yapma iddiasında bulunmuyor. Nasıl talimat vereceğimizi bildiğimiz her şeyi yapabiliyor” (italikler Lovelace’a aittir)25
25 Alan M. Turing, a.y.
Bu noktada nasıl talimat vereceğimizi bildiğimiz her şeyi makineye yaptırabileceğimiz söylemi çok kapsamlı bir söylemdir. Hiçbir şekilde programlanmamış bir makine donanım olarak tam olsa da kendi kendine bir işlem yapma kabiliyetine sahip değildir. Makineye verilen talimatlar onu öngöremeyeceğimiz çıktılar üretebilecek şekilde programlamayı da içerebilir. Bu açıdan baktığımızda Lovelace ve Turing’in makinelerin yapabilecekleri ile ilgili düşünceleri birbirlerinden çok da uzak değildir.
Turing’de devamında bu argümanın daha iyi bir çeşitlemesi olarak “bir makinenin bizi asla şaşırtamayacağı” düşüncesini ele almayı önerir. Buna göre bir şeyin şaşırtıcı olması yani sürpriz olarak kabul edilmesi için “yaratıcı zihinsel birhareketin” gerekliliğinden bahseder. Makinelerin sürprizlere yol açamayacağı görüşünün ise özellikle matematikçilerin ve felsefecilerin düştüğü bir yanılgı olduğunu söyler. Bu yanılgının sebebini ise “herhangi bir gerçek, bir akla sunulduğu zaman tüm sonuçların aynı anda akla geleceği varsayımı”26 olarak açıklar. Bu varsayımın çeşitli koşullar altında faydalı fakat doğru olmadığını dile getirir. Burada tüm sonuçların aynı anda akla geleceği varsayımının yanlış olduğunu söyleyerek Turing’in insan zihninin sınırlarını vurguladığını görüyoruz. Günümüzde makine öğrenmesi ve derin öğrenme yöntemleriyle alınan sonuçlar da makinelerin insanları şaşırtabileceğini en basit şekilde oyunlar üzerinde göstermiştir. Çalışmamızın son bölümünde buna ilişkin örnekler yer almaktadır.
26 Alan M. Turing, “Computing Machinery and Intelligence”, s. 448.
2.1.7 Sinir Sisteminin Sürekliliği Argümanı
Bu argümanda; bilgisayarın bir kesikli durum makinesi, sinir sisteminin ise birsürekliliğinin olduğu iddia edilir. Turing de makalesinde düşünmenin kesintisiz olduğunu, bilincin parçalı değil bütüncül, makinelerin ise kesikli yani süreksiz olduğunu kabul eder. Yine de taklit oyununda bunun bir önemi olmadığını ekler. Birdüşüncenin sürekli bir sistemde mi, kesikli bir sistemde mi üretildiğinin nasıl bir önemi olabileceğini sorgular. Burada önemli olan noktanın, düşüncenin üretilmesi olduğunu vurgular.
1950'de kuantum fiziğinde yaşanan gelişmeler sayesinde, uzay ve zamanın da, enerjinin de yapısı kesikli olarak tanımlanmıştı. Turing’in neden nöron aktivitelerine süreklilik özelliğini atfettiği bilinmiyor. Bu konunun aydınlatılması için dönemin nörobilim kabullerini incelememiz gerekebilir. Şimdilik, ortaya atılan çalışmaların doğru olmasına rağmen kabul görmediği bir dönem olabileceğini tahmin ederek devam edeceğiz. Çünkü modern sinir bilimin kurucusu olarak kabul edilen Santiago Ramon y Cajal27 (1852-1934) nöron doktrini üzerine ilk makalesini 1888 yılında “Kuşların Sinir Merkezlerinin Yapısı” ismiyle yayınlamıştır. Bu makalede ilk defa sinir hücrelerinin birbirleri ile sürekli değil kesintili temaslar ile haberleştikleri ileri sürülmüştür. Santiago Ramon y Cajal’ın çalışmaları sinir bilimlerinde önemli bir dönüm noktasıdır. Bu çalışma sayesinde sinir sisteminin de diğer tüm dokulardaki gibi tek tek hücrelerden oluştuğu ve sürekliliği olmadığı gösterilmiştir. Cajal 1906 yılında sinir sisteminin yapısı konusundaki Nöron Doktrini28 araştırmaları üzerine Camillo Golgi ile birlikte Nobel Tıp/Fizyoloji Ödülü’nü almıştır.29
Böylece canlılardaki sinir sisteminin sürekli olmadığı ve bu mevcut süreksiz yapının beynin makinelerde modellenememesi sorununa sebep olamayacağı anlaşılmaktadır.
27 19. yüzyıl İspanyol bilim insanı ve modern nörobilimin kurucusu kabul edilen Santiago Ramon yCajal, beynin yapısı ile ilgilenen ve çözen ilk araştırmacılardandır. Bununla birlikte Cajal, nöronal morfoloji, haberleşme ve gelişimi ile ilgili bulgularıyla da sinirbilim dünyasında yeni bir devrinbaşlamasına öncülük etmiştir. Ayrıca bkz. Gordon M. Shepherd, Foundations of the Neuron Doctrine, Oxford University Press, 2015, s. 127.
28 Nöron Doktrini, nöronların birbirinden ayrı, tekil hücreler olduğunu ileri sürer. Doktrine göre, nöronlar biyokimyasal olarak birbirlerinden bağımsız çalışmaktadır. 1873’de Camillo Golgi gümüş nitrat ve potasyum dikromat’ın bir araya gelerek sinir hücrelerinin zarlarına gümüş kromat partikülleri halinde bağlanabildiğini keşfetmişti. Bu da nöronların sarı zemin üzerinde görünebilir halegelmesini sağlıyordu. Ayrıca bkz. Gordon M. Shepherd, Foundations of the Neuron Doctrine, Oxford University Press, 2015, s. 141.
29 Simge Aykan Zergeroğlu- Erhan Nalçacı, “Santiago Ramon y Cajal ve Nöron Doktrini”, Turk J Neurol, 2015, Sayı:21, s.81-84. (Çevrimiçi) https://www.journalagent.com/tjn/pdfs/TJN_21_3_0.pdf12 Aralık 2019.
2.1.8 Davranışların Teklifsizliği Argümanı
Turing’in makalesinde yer verdiği diğer bir karşı çıkış, davranışların informelliği argümanıdır. Bu argümana göre, insanlar sürpriz yapar ve şaşırtırlar çünkü davranışları informeldir, planlı programlı değildir. Ama makineler sürpriz yapmaz, formeldir, nasıl programlanmışsa öyle davranır. Bu argüman aslında insanın özgür iradesi olduğu varsayımına dayanır. Davranışların nedensel bağlamı olmadığını, bir özden belirlenimsiz olarak ortaya çıktığını savunur. Turing ise, insan davranışlarının tüm karmaşıklığına rağmen formel altyapıları olacağını varsayar. Makinelerde de aynı karmaşıklıkta formel yapılar kurulursa, sonuçları dışarıdan informel olarak algılanabilir, yani makineler de bizi şaşırtabilir der. Turing’e göre, herşey formeldir, ancak formellik çok karmaşık olunca ortaya öngörülemeyen davranışlar çıkabilir.
2.1.9 Duyu Ötesi Algı Argümanı
Bir diğer karşı çıkış, duyu ötesi algı argümanıdır. Bu argüman insanın altıncı hissinin olduğunu ve telepati yapabildiğini, makinelerde ise böyle bir özelliğin bulunmadığını iddia eder. Turing bu argümana cevap olarak önce telepatinin; beynimizin, bizim fizikselliğini bilmediğimiz bir fonksiyonu olabileceğini ve bu fonksiyonun nedensel yapısını çözersek makinelere de telapatiyi öğretebileceğimizi öne sürer.
Turing makalesinde düşünebilen bir bilgisayar olasılığını dile getirir. Mantıksal bir biçime yerleştirilebilen her önermenin bilgisayarlar tarafından taklit edilebileceğinden yola çıkar. İnsan seviyesinde bir akılyürütmenin yapay olarak gerçekleştirilebilmesi için sağduyu akıl yürütmesinin formelleştirilmesi gereklidir.1 Bilgisayar bilimci John McCarthy de “Sağduyu Sahibi Programlar” makalesinde benzer bir olasılıktan bahseder. Ona göre sağduyu bilgisi ve karar alma süreci mantıksal bir biçime yerleştirilebilir.2
1 Vedat Kamer, “Yapay Zeka ve Monoton Olmayan Mantık”, İstanbul Üniversitesi, 2009, s.35. (Çevrimiçi)http://acikerisim.istanbul.edu.tr/bitstream/handle/123456789/27879/45445.pdf?sequence=1&isAll owed=y, 12 Aralık 2019.
2 John McCarthy, "Programs with Common Sense", Teddington Conference on the Mechanization ofThought Processes, 1958. (Çevrimiçi) http://www-formal.stanford.edu/jmc/mcc59.pdf, 12 Aralık2019.
2.2 Çin Odası Deneyi
Turing’den sonra, ortaya koyduğu bir düşünce deneyiyle literatüre önemli bir katkısı olan John Searle (1932-), 1980 yılında Çince Odası deneyini açıkladığı makalesini yayınlamıştır.3 Bu deneyde kapalı bir odanın içinde bulunan ve Çince bilmeyen bir insan posta deliğinden Çince mesajlar almaktadır. Odanın içinde kendisine rehberlik eden Çince sembollerle ne yapacağını söyleyen bir kural kitabı vardır. Bu kitapta kurallar tamamen formel olarak ifade edilmiştir. Örneğin; “bu şekli (Çince sembol) gördüğünde karşılığında şu şekli ver” gibi. Bu formel önermeler o kadar doğru şekilde çalışıyordur ki karşısında bir Çinli de olsa odanın içindeki insanın Çince bildiğinden emin olabilmektedir. Searle’e göre bu insan Çince bilmeden bunu başarmaktadır. Ona göre bir dili anlamak yada zihinsel başka durumlara sahip olmak formel sembollerle yönergeleri yerine getirmekten daha fazlasını içerir. Yani sentaks, sayıların dizimi ya da sembollerin manipülasyonu, semantik (anlamın üretilmesi) için yeterli değildir. Aslında Çin odası deneyi Çince yapılmış bir Turing testidir diyebiliriz, burada testi geçmiş olma durumunun düşünen makineler konusunda hala ikna edici olmadığına dikkat çekilir. Searle’e göre Turing testini geçen bir makine için “düşünüyor” ya da “anlıyor” diyemeyiz.
3 John Searle, Minds, Brains, and Programs, The Behavioral and Brain Sciences, 1980, 3, s.417-457.
Fakat farklı bir bakış açısıyla, Çince odası deneyinde odada kapalı olan insanın bir sinir hücresi olduğunu düşünebiliriz. Bu sinir hücresinin sadece bir “aracı” olarak görev yaptığını yani beyindeki bütünlüğün bir parçası olduğunu ve bu durumda Çinceyi tek başına -kendi bilinciyle- anlaması gerekmediğini söyleyebiliriz.
Zihin işlemlerinin sayısal hesaplamalardan ibaret olduğu kabulü bir yana beynin bir bilgisayar mı olduğu, yoksa farklı unsurları birleştirici bir makine mi olduğu ya da beynin paralel bir bağlantı sistemine mi sahip olduğu konusunda fikir birliği yoktur.4 Bu noktada zihnin niteliği problemi ortaya çıkar, buradan da zihninnasıl tanımlandığı, üretilebilir olup olmadığı sorusunun cevabı şekillenecektir. Ancak zihin denilen şeyin ne olduğu konusunda kesin bir veri mevcut değildir. Bu nedenle konuya çeşitli açılardan yaklaşan farklı tanımlamalar ortaya çıkmıştır. Zihnin nasıl tanımlandığı, onun ne olduğunu ortaya koyacaktır. Dolayısıyla herhangi bir zihin tanımı; onun üretilebilir bir şey olup olmadığını içeren bir açıklama sunacaktır. Günümüzde bilgisayar bilimleri insanın insan olma özelliğinin ve zekâsının kaynağını beyin olarak kabul eder ve beyin sadece biyolojik bir bilgisayar olarak ele alınır. Buradan yola çıkılarak dijital bilgisayarlar ile yapay bir beyin elde edilmesi araştırmaları yapılmaktadır. Örneğin bir görüşe göre nanobotlar5 kullanılarak beyin çalışmakta iken onun bütün beyin hücrelerini (nöronlarını) içeren bir haritasını görüntülemek mümkündür. Bu haritadaki verilerle ve tersten inşa (reverse engineering) yöntemi ile beynin yapısını ve beyinde düşüncenin nasıl oluştuğunu anlayabileceğimiz iddia edilir.
4 John Searle, Zihnin Yeniden Keşfi, Çev. M. Macit, İstanbul: Litera Yayıncılık, 2004, s. 244-46.
5 Nanobot: Nanorobot olarak da bilinen bu küçük robotlar, başka bir cihaza bağlanmadan mikroskobik düzeyde kendi kendine çalışabilen cihazlardır. Bu malzemelerle molekül boyutunda bir şeyler inşa edilebilir ya da moleküllerin yapısı değiştirilebilir. Ayrıca bkz. Chris P. Toumey, Nanotech and the Humanities: An Anthropologist Observes the Science of Atoms and Molecules, Cambridge Scholars Publishing, 2019, s.95.
2.3 Bilinç Tartışması
Kendimizi ve bulunduğumuz ortamı anlamak istediğimizde, çoğunlukla zihinsel ve fiziksel durumlar arasında bir fark olduğunu düşünürüz. Zihinsel durumları düşünme, hayal kurma, hissetme, arzu etme, karar verme vb. ile ilişkilendiririz. Fiziksel durumları ise bedensel, biyolojik ve maddi yapılarla ilişkilendiririz. Bu çerçevede bilinç, zekâyı da kapsayan zihinsel bir durum olarak değerlendirilir. Bilincin varlığı çoğu düşünce sisteminde kabul edilmekle birlikte yeryüzünün önemli bir bölümünü oluşturan madde ile bilincin ortaya çıkışı arasındaki bağıntı henüz tüm yönleriyle saptanamamıştır. Bu yüzden de beyin gibi fiziksel bir varlığın, nasıl bilinç denilen karmaşık duygu ve düşünce kalıplarına neden olabildiği önemli tartışmalara sebep olmaktadır.
Zihin-beden sorunu ilk olarak René Descartes’ın (1596-1650) zihin vebedenin birbirinden tamamen ayrı olduğunu iddia ettiği iki töz kuramı ile ifade edilmiştir:
“...beden ile ruh arasında, bedenin mahiyeti icabı daima bölünmesi, ruhun ise tamamen bölünmemesi yüzünden büyük bir fark görüyorum. Zira gerçekten ruhumu, yani yalnız düşünen bir şey olan kendimi gözden geçirdiğim zaman, onda hiçbir bölüm göremiyor, aksine kendimi tek ve tam bir şey olarak idrak ediyorum. Her ne kadar bütün ruh tamamıyla bedenle birleşmiş gibi görünse de bir ayak, bir kol veya vücudumun başka bir parçası bedenimden ayrıldığı zaman ruhumdan hiçbir şey ayrılmadığı muhakkaktır.”6
Descartes, zihin ya da bilinci, duyu organlarımızla algıladığımız dünyadan bağımsız bir kavram olarak düşünmektedir. Bu yüzden, zihin ve maddeyi iki ayrı töz olarak tanımlar. Descartes’a göre düşünme denildiğinde bilinçli düşünme kastedilir çünkü ona göre düşünme bilinçten bağımsız olarak gerçekleştirilemez. Düşünen varlık kendi düşüncelerine ve bilincinin içeriğine diğerlerinden farklı olarak; ayrıcalıklı ve hatasız bir şekilde erişebilir.7 Bu yüzden de insanın kendi düşüncesini anlayamaması ya da kendi düşüncesini bilmemesi mümkün değildir. Descartes “Düşünüyorum o hâlde varım.” derken de var olmanın kanıtı olarak bu hatasız erişime işaret etmiştir.
6 René Descartes, İlk Felsefe Üzerine Metafizik Düşünceler, (çev. Mehmet Karasan), MEB Yayınları, İstanbul, 1998, s. 256.
7 Descartes, a.g.e., s. 245; Ayrıca bkz. Erdinç Sayan, Bilinç, Felsefe Ansiklopedisi, c. 2, (ed. AhmetCevizci), Etik Yayınları, İstanbul, 2004, s. 574-585.
Turing’in 1950 yılında yazmış olduğu Hesaplama Makineleri ve Zekâmakalesinden bu yana makinelerin düşünebilmesi tartışmalarının sürmesinin önemli bir nedeni de hala bilincin tanımı ve kapsamıyla ilgili genel geçer bir görüş birliğinin olmamasıdır. Bilincin tanımı ve kapsamı hakkında ortak bir görüş olmasa da yapay zekâ alanında yapılan bilinç tartışmalarının anlaşılması ve geliştirilebilmesi için “yapay bilinç” ile ilgili yapılması gereken temel ayrımlardan biri zayıf ve güçlü yapay zekâ arasındaki ayrımdır. Bu yüzden yapay zekâ çalışmalarında bilinç konusu ile ilgili çeşitli görüşlere yer vermeden önce bu ayrımı netleştirmeye çalışacağız.
Bu ayrıma göre güçlü yapay zekâ kuramı; dijital bilgisayarların, anlama, akıl yürütme ve düşünme gibi bilişsel yeteneklere sahip olacak şekilde programlanabileceğini ileri sürmektedir. Buna göre uygun bir şekilde programlanmış bir bilgisayar bir zihinle özdeştir ve bilinç sahibidir denebilir. Zayıf yapay zekâ kuramı ise dijital bir bilgisayarın vermiş olduğu çıktılar ne kadar anlamlı ya da tutarlı görünse de, bu çıktıların bilgisayarın düşünme, akılyürütme ve anlama yetilerine sahip olduğu anlamına gelmediğini ve bir bilince sahip olamayacağını ileri sürmektedir.8 Güçlü yapay zekâ kuramında geçen “uygun bir şekilde programlama” işlemi bir bilgisayara, insandaki gibi bir bilince sahip olduğundan şüphe edilmeyecek şekilde anlama kapasitesi kazandırmaktır. Zayıf yapay zekâ kuramında ise, dijital bilgisayarların sadece insanın çıkarım yapma eylemini, mekanik olarak taklit ettiği ve insanın programlamadığı herhangi bir davranışta bulunamayacağı savunulmaktadır.
Alan Turing güçlü yapay zekâ kuramının öncülerinden kabul edilir fakat o, makalesinde bilinç kavramını “gizemli” olarak nitelendirmiş ve taklit oyunu için böyle bir kavramı tanımlamaya ihtiyaç olmadığını söylemiştir.9 Sonrasında da taklitoyunu ile makinelerin düşünebilmesi olasılığını, oyunu geçme başarılarına göre değerlendirmeyi önermiştir.
J. Searle’e göre ise makineler, ancak bilince sahip olduklarında insanın yerini alabilirler ve dijital bilgisayarlar ile bilinci olan bir makine üretmek mümkün değildir. Güçlü yapay zekânın oluşturulabilmesi için ön koşulun bilinç olduğunu düşünen Searle, bilinç üzerinde çalışmadan beyin ile ilgili çalışmanın, sindirimi açıklamadan mideyi tanımlamaya benzediğini söyleyerek bilincin beyni çözümlemedeki önemini vurgulamıştır.10 Bilincin bilimsel bir tanımının henüz yapılamayacağını kabul ettiği halde bilinç konusunda konuşmak için bir tanım bildirmesi gerektiğini de belirten
8 Kamuran Gödelek, Zihin Felsefesi, Eskişehir: Anadolu Üniversitesi Yayınları, 2011, s.119.
9 Alan M. Turing, “Computing Machinery and Intelligence”, s. 444.
10 John Searle, Zihnin Yeniden Keşfi, s.115.
Searle’ün 2013 yılında katıldığı bir konferansta yapmış olduğu bilinç tanımı ise şu şekildedir:
“...İnsanlar her zaman bilinci tanımlamanın ne kadar zor olduğunu söylerler. Bence eğer bilimsel bir tanımlama için uğraşmıyorsanız, bu tanımı yapmakdaha kolay. Biz bilimsel bir tanımlama için hazır değiliz, ama işte aklıselim birtanım: Bilinç tüm duygu durumlarını, duyarlılığı ya da farkındalığı içerir. Rüyasız bir uykudan uyandığınız an başlar ve uykuya dalana kadar ya da ölene kadar ya da bir şekilde bilinçsiz hale gelene kadar devam eder. Rüyalar da bu tanımda, bilincin bir şeklidir...”11
Searle konuşmanın devamında, bu tanımda geçen; rüyasız bir uykudan uyandığımız anda başlayan ve uyku, koma, ölüm vs. gibi durumlarda yok olan bilinçli olma halinin, varlığı ve yokluğunu da basit bir örnekle açıklar. Ona göre bütün bilinç durumlarımız, beyindeki alt seviye nörobiyolojik süreçler sayesinde oluşur ve bu süreçler ancak suyun akışkanlığını kaybetmesi kadar gizemli ve doğaldır. Bir kavanozun içinde bulunan suyun yeterince soğutulduğunda akışkanlığını yitirmesi, yani moleküler yapısının sıvı halden katı hale geçmesi gibi bilinçli ve bilinçsiz olma durumları arasında da beyinde böyle bir fiziksel geçiş söz konusudur.12
Bilinci fiziksel dünyada yer alan doğal bir fenomen olarak tanımlayan Searle için bilinç, ikicilikteki gibi ayrı bir töz olmayıp beynin sahip olduğu biyolojik bir süreçtir. Bu açıdan Searle, zihni ayrı bir töz olarak kabul eden ikiciliği bilinç tartışmaları için faydalı bulmaz, fizikselciliği ise indirgenemez olan öznel, farkında olma durumlarını kabul etmemesi açısından eksik bulur. Dolayısıyla Searle’e göre, ikicilik bilinç problemini çözülemez yaparken, fizikselcilik bu problemin varlığını reddetmektedir.13 Böylece Searle, hem ikiciliği hem de fizikselciliği farklı açılardan eleştirerek bu iki görüşe alternatif “biyolojik doğalcılık” yaklaşımını ileri sürer. Bu yaklaşımın diğer görüşlerden en belirgin farkı ise bilinç ve beyin arasındaki indirgemenin nedensel bir indirgeme olmasıdır.14 Böylece biyolojik doğalcılık görüşü kapsamında, bilinç biyolojik bir süreç olarak görüldüğünden, yapay bir beynin üretilmesi ve üretilen bu beyinde bilincin oluşmasının önünde ilkesel olarak bir engel yoktur.15 Buna rağmen biyolojik doğalcılığın kastettiği şey, bilincin doğallaştırılması, yani apaçık herkes tarafından eşit anlaşılabilecek şekilde ortaya konulabilmesi değildir. Searle’e göre zihnin doğallaştırılmasından bahsedilirken onun öznel yanı reddedilmektedir, fakat biyolojik doğalcılıkta, bilinç öznel ve niteliksel özellikleriyle birlikte doğal bir fenomen olarak kabul edilir.16 Biyolojik doğalcılıkta bilincin en belirgin özelliği herkesçe anlaşılabilecek şekilde açıklanamıyor olmasıdır.
11 John Searle, Philosopher, Our Shared Condition Consciousness (Paylaştığımız Durumumuz- Bilinç),TEDxCERN, 2013, (Çevrimiçi)https://www.ted.com/talks/john_searle_our_shared_condition_consciousness/transcript?language= tr&hc_location=ufi (04:04) 12 Aralık 2019.
12 Ted Talk devamı (04:55) Ayrıca bkz. J. Searle, Toplumsal Gerçekliğin İnşası, Çev. M. Macit & F. Özpilavcı, İstanbul: Litera Yayıncılık, 2005, s.37.
13 J. Searle, Zihnin Yeniden Keşfi, s.47.
14 Searle, nedensel indirgemeyi şu şekilde açıklar: “Eğer bir A fenomeni nedensel olarak B fenomenine indirgenebiliyorsa, A’nın tüm davranışları B’nin davranışları tarafından açıklanabilir ve A’nın B’den fazla hiçbir nedensel gücü yoktur. Ontolojik indirgeme ise şu anlama gelmektedir: Sadeceve sadece A hiçbir şeyse ve yalnızca B ise, A fenomeni, B fenomenine ontolojik olarak indirgenebilirdir. Fizikselcilerin yaptığı ontolojik indirgemedir bu noktada zihin, bedene ontolojikolarak indirgenir ve zihnin varlığı yok sayılır. Böyle bir ontolojik indirgeme kabul edilemezdir” (SearleZihnin Yeniden Keşfi, s.119.)
15 J. Searle, Zihin, Dil, Toplum, Çev. A. Tural, İstanbul: Litera Yayıncılık, 2006, s.64.
16 J. Searle, Bilincin Gizemi, Çev. İ. K. İçyüz, İstanbul: Küre Yayınları, 2018, s.18.
Searle, güçlü yapay zekânın sınırlarını gösteren düşüncelerini ise Çin odası argümanı ile açıklamıştır. Bir önceki bölümde bahsettiğimiz gibi Searle bu deney ile Çince bilmeyen birinin, bir Çinliyle diyaloğa girdiğinde yeterli materyale (kendi anadilinde bir kurallar kitabı ve Çince tabelalar) sahip ise sorulan sorulara cevapolarak anlamlı Çince çıktılar üretebileceğini, fakat bu anlamlı çıktıların, o kişinin Çinceyi bildiği anlamına gelmediğini vurgulamıştır.
Searle’ün bir bilgisayar programının çalışma şeklini örnek alarak ortaya koyduğu bu düşünce deneyinde odada bulunan kişi Çince bir soruya Çince cevap verebilmesine rağmen verdiği cevabın içerik/anlam olarak ne ifade ettiğini bilmemektedir. Bu açıdan Searle’e göre, bilgisayar programlarında yazılım açısından bir sözdizimi (sentaks) vardır; fakat anlam (semantik) bulunmamaktadır. Bu yüzden de bilgisayarlar algılama, anlama ve düşünme gibi özelliklere sahip değildir yani Searle’e göre bilgisayarlar Çinceyi ve bunun gibi diğer bilişsel formların hiçbirini bu deneyde olduğu gibi gerçek anlamda anlayamayacaklardır.17
Görüldüğü gibi Çin Odası argümanını oluştururken Searle’ün kullandığı üç aksiyom (temel varsayım/ön kabul) vardır. Bunlardan ilki bilgisayar programlarının sözdizimsel oluşudur. Diğeri; insan beyninin, bilgisayar programına benzemeyen birzihinsel içeriğe (semantik/anlam) sahip olmasıdır yani sözdizimsel olmamasıdır. Üçüncü aksiyom ise bu ilk iki aksiyomu birleştirir niteliktedir: “Sözdizim, ne tek başına anlam için yeterlidir ne de anlamın kurucusudur.”18 Searle’e göre buradan şu sonuca ulaşılır: Programlar ne zihin için yeterlidir ne de zihnin kurucusudur. Çin odası deneyindeki bu üç aksiyomun hatalı olup olmadığı hala tartışılmaktadır. Bu aksiyomlardan herhangi birinin hatalı olduğunu ispatlayabilmek için güçlü yapay zekânın oluşturulması gerekiyor gibi görünmektedir. Şimdilik böyle bir ispat yöntemi mümkün olmasa da tam tersi olan yani güçlü yapay zekânın dijital makineler ile oluşturulamayacağı iddiasını da kabul etmek yanlış olacaktır. Searle’ün de biyolojik doğalcılık görüşünü açıklarken ifade ettiği gibi yapay bir beynin üretilmesi ve üretilen bu beyinde bilincin oluşmasının önünde ilkesel olarak bir engel yoktur. Bilincin beyinde var olduğu düşünülen bir fenomen olduğunu göz önünde bulundurduğumuzda beynin tüm katmanlarıyla yapısal olarak taklit edilmesi ve nöronlar arasındaki bağlantıların elektrik akımları ile birlikte modellenebilmesi mümkün olduğunda tüm diğer işlevlerle birlikte bilinç oluşumunda bilimsel olarak açıklanabilmesi mümkün görünmektedir. Ancak bilinç bu şekilde nesnel hale getirilse bile aslında insan beyni modellenerek oluşturulduğu için yine de öznel bir içeriği olacaktır.
Patricia S. Churchland (1943-) ve Paul M. Churchland (1942-) “Bir Makine Düşünebilir mi?”19 adlı makalelerinde Searle’ün “Söz dizim anlam için yeterli değildir” varsayımının hatalı olabileceğini göstermek için yeni bir argüman ortaya atarlar. Churchland çifti argümanlarını sunmadan önce Searle’ün şüpheciliğinin bilim tarihinde daha önce de yaşandığından bahsederler ve benzer durumlarla ilgili örnekler verirler. Bu örneklerde bazı bilim insanlarının bazı durumları olağanüstü olarak değerlendirdiği ve kabul etmekte zorlandığı yine de bilimsel deneylerle gerçeklerin ispatlandığı anlatılır. Benzer olarak Searle’ün çok sınırlı bir yapıda olan düşünce deneyinden, formel sistemlerin anlama gerçekleştiremeyeceği sonucunun da çıkarılmaması gerektiği vurgulanır. Churchland çiftine göre semantik içeriğe sahip güçlü yapay zekâ için beyne benzer yapıda paralel ve ilişkisel mimariye sahip sistemler kullanılmalıdır. Bahsedilen bu sistemler günümüzde mimari gelişimi devam eden insan beynindeki sinir ağlarını örnek alan yapay sinir ağlarıdır.
17 J. Searle, “Is the Brains Mind a Computer Program?”, Scientific American, Ocak 1990, s.26-31.
18 J. Searle, a.e., s. 27.
19 Patricia S. & Paul M. Churchland, “Could a Machine Think?” , Scientific American, Ocak 1990, s.32- 37. (Çevrimiçi) http://sils.shoin.ac.jp/~gunji/AI/CR/sciam90couldamachinethink.pdf, 12 Aralık 2019.
Searle’ün şüpheciliğini ve öznelliğin sözdizimsel bir sistem ile sağlanamayacağı iddiasını destekleyen isimlerden biri de Thomas Nagel (1937-) dir. Nagel “Yarasa Olmak Nasıl Bir Şeydir?” isimli makalesiyle öznelliğin bir makineye aktarılamayacağı görüşünü savunmaktadır. Nagel’e göre, yarasanın nörofizyolojisi herkese açıktır, hatta bu bağlamda bir Marslı, insan beyni hakkında, insandan fazla bilgiye sahip olabilir ya da gökkuşağındaki fiziksel süreci de anlayabilir. Fakat birMarslı, gök kuşağının, insan beyninde nasıl bir anlam uyandırdığını bilemez. Dolayısıyla, içinde bulunduğumuz durumdan çıkarım yapmak bir yarasa olmanın nasıl bir şey olduğunu düşünmeyi içeriyorsa, bir yarasa olmadığımız sürece bu çıkarım tam ve eksiksiz olmayacaktır. Bu yüzden yarasa olmanın nasıl bir şey olduğunu düşünürken bu “olma durumu”na dair şematik bir fikirden fazlasını oluşturmamız mümkün değildir. Dolayısıyla deneyimi yaşayan kişi, diğer kişiden ne kadar farklıysa, o kişi olma deneyimini anlamak da o oranda düşük olacaktır.20
20 Thomas Nagel, Zihin ve Evren (Çev. Ö. Ç. Aksoy), İstanbul: Jaguar Kitap, s.151.
Nagel, deneyimin öznel karakteri ve iç tecrübeyle fiziksel durumlar arasındaki farkı ortaya koymak için ilginç bir örnek verir:
Bir an için siz bir çikolatalı gofret yerken beyninizi yalayarak çikolatayı tatma tecrübenizi gözlemlemeye çalışacak kadar çılgın bir bilim adamı olduğunu varsayalım. Büyük olasılıkla, beyniniz ona hiç de çikolataya benzer bir tat vermeyecektir. Öyle olsaydı bile, bu bilim adamı, yine de, zihninizin içine bakıp çikolatayı tatma tecrübenizi gözlemlemede başarısız olurdu. O, kendi çikolata tadına siz de kendi çikolata tadınıza sahipsinizdir.21
Buradan şöyle bir sonuç çıkarılabilir: Bilinç nesnel bir gözlem konusu olamaz. Fakat bu sonuçla bilim metodolojisi çatışmaktadır çünkü bilim nesneldir; tüm olgular üçüncü kişilerin gözlemine açıktır. Bilinç kavramı bu metodoloji ile ele alınırsa ‘bilinç’ açıklanamaz. Buna göre eğer bir bilgisayarın bir bilince sahip olması mümkün olursa bilince sahip bir bilgisayar olmanın nasıl bir şey olduğunu biz bilince sahip bir insan olarak tam ve eksiksiz bir şekilde algılayamayabiliriz.
Zihnin ve zihinsel fenomenlerin açıklanmasında ikiciliğin ve fizikselciliğin yetersiz olduğunu göstermek için ortaya atılan bir diğer düşünce deneyi de Ned JoelBlock’un (1942-) Çin Ulusu deneyidir.22 Bu deneyde Çin nüfusu, canlı beynindeki nöron bütünlüğü olarak düşünülür aralarında kurulan bağlar nöronlar arasında kurulan bağlantılara benzetilir. Deneyde öncelikle her bir Çinliye aranacaklar listesinden telefon numaraları dağıtılır ve kararlaştırılmış bir zamanda belirli kişiler kendi listelerindekileri arayarak deneyi başlatırlar. Listedeki bir Çinlinin telefonu çaldığında o da kendi listesindeki kişileri arar ve deney bu şekilde devam eder. Bu deneyde telefon aramaları, nöronların birbirleri arasındaki iletim ile aynı işlevsel rolü oynamaktadır. Ve Searle ile benzer olarak bu deneyden de şöyle bir sonuç çıkarılır: eğer fizikselcilik doğru kabul edilirse Çin nüfusunun kolektif olarak bir zihinsel hal içinde olduğunu söylememiz gerekir ve eğer söyleyemezsek fizikselcilik yanlıştır.
21 Thomas Nagel, Her Şey Ne Anlama Geliyor? (Çev. H. Gündoğdu), İstanbul: Paradigma Yayınları,2004: s.21.
22 Ned Block, “Troubles with functionalism”, Minnesota Studies in the Philosophy of Science 9:261- 325, 1978.
Searle deneyini açıklarken güçlü yapay zekâyı hedef aldığı için bilinirliği artmış olsa da Block’un deneyi duruma farklı bir açıdan bakmaya daha elverişlidir. Çünkü eleştirel bir yaklaşımla da olsa, Çin nüfusunun kolektif olarak bir zihinsel haliçinde olduğunu düşünme imkânı verir. Kanımızca Çin nüfusu kolektif olarak bir zihinsel hal içindedir diyemesek de, Çin nüfusunun bir zihinsel haller bütünü sonucunda bir eylemde bulunduğu (arama listelerindeki tüm insanların aranması) söylenebilir. Her bir Çinli temelde kendine ait bir hedefi tamamlamak için harekete geçer ve bu hareket dalga halinde tüm ülkeye yayılır. İşlem tamamlandığında bazı Çinliler arasında bağlantı kurulmuş olur. Ve sonuç olarak Çin ülke olarak ortak bireylemde bulunmuş olur, deney tamamlanır. Arama listeleri tek bir Çinli’nin tüm geri kalan Çinlileri arayabileceği şekilde ayarlanıp zamanlama planlamasıyla hatların meşgullüğü engellenerek deney büyütülebilir. Çünkü bir telefonda, herhangi bir başka telefonla bağlantı kurulması imkânı mevcuttur. Bu geometrideki bir noktadan sonsuz doğru geçer aksiyomu ile de benzerlik göstermektedir. Geometri ile bağlantı kurmamızın sebebi telefonları olan Çinlilerin beyindeki nöronlara benzetilmesi ve beyindeki nöronların bağlantılarının güçlü ve zayıf oluşuna göre algılarımızın hafızamızda yer edinmesi böylece öğrenmenin gerçekleşmesidir. Nöron sayısı ve bağlantıları sürekli olarak değiştiği için beyindeki nöronlar arasında sonsuz farklı kombinasyonla bağlantı kurulabilir. Düşüncelerimizin bir sınırının olmayışı ve beyin hakkında yapılan bilimsel çalışmaların sonucunda neden mide hakkında edindiklerimiz kadar net veriler elde edemediğimizin bir göstergesi de bu bağlantı kombinasyonlarının sayısının sonsuz olması olabilir. Nagel ve Searle’ün öznellik vurgusu da, beyinde yer alan bu bağlantıların bireye özgülüğüne yani genler ve deneyimler gibi etkenlerin beyinde benzersiz kombinasyonlar oluşmasına sebep olmasıyla açıklanabilir.
Günümüzde tıp bilimindeki gelişmeler ve yapay zekâ alanındaki teknolojik ilerlemeler sayesinde insan beyni ve makineleri buluşturan deneyler yapılabilmektedir. Aynı zamanda yapay zekâyı günlük yaşama dâhil etmek için (ör. Otonom araçlar, güvenlik kamera sistemleri vb.) görüntü tanıma yöntemleri ön plana çıkmaktadır. Bilinç kavramının bugün kullandığımız halini almasında önemli katkıları olan düşünürlerden biri olan John Locke’un (1632-1704) insanda görüntü tanıma ile ilgili söyledikleri de bu açıdan dikkate değerdir.
Locke’un görüntü tanıma ile ilgili düşüncelerini daha iyi anlayabilmek için öncelikle bilinç ve algılama hakkındaki görüşlerine yer vereceğiz. Locke, “İnsanın Anlama Yetisi Üzerine Bir Deneme” adlı kitabında bilinç kavramını, zihinsel duyumlarla ve öznellikle ilk kez ilişkilendiren düşünür olarak bilinir. Locke, ‘insanın kendi zihninden geçenleri algılaması’23 olarak tanımladığı bilinç kavramı için algılamanın önemini şu şekilde ifade etmiştir:
“Algılama, idelerimiz alanında kullanılan ilk zihinsel yeti24 olduğundan iç duyumdan edindiğimiz ilk ve en yalın idedir ve bazılarınca genel anlamıyla “düşünme” diye de adlandırılır. İngilizcede “thinking” (düşünme) zihnin kendi ideleri üzerinde etkin olarak yer aldığı bir işlem türüdür; bu sırada herhangi bir şeyi dikkat harcayarak irdeler. 25Algılama zihnin çoğunlukla edilgin olduğu bir alandır ki algıladığı şeyi algılamaktan kaçınamaz.”26
Locke algılamanın öznelliğini ise sadece zihninde olup bitenleri duyan birinin algılamanın ayırtına varabileceğini fakat bu duyumu almayan birine ne kadaranlatılırsa anlatılsın herhangi bir kavrama kavuşamayacağını iddia ederek ifade etmiştir. Yani insanın kendi zihni ile kurduğu ayrıcalıklı ve hatasız erişime, öznelliğe dikkat çeken tüm diğer düşünürler gibi Locke da dikkat çekmiş ve açıklamaya çalışmıştır. Ona göre görme yetimiz de görülen nesnelerin ortak olması sebebiyle nesnel gibi algılanmakta fakat belirli noktalarda öznellik ve illüzyonlar dikkat çekmektedir. Locke önyargı ile görme yetisi üzerine şunları söylemiştir:
“Önyargı görme yetisi ile edinilen idelerimizde olağandır. Tüm duyularımızın en karmaşığı olan görme duyusu zihinlerimize yalnızca bu duyuya özgü olan renk ve ışık ideleri ile ışık ve renklerdeki çeşitlilikler, uzay, şekil ve harekete ilişkin çok farklı idelerilettiğinden alışkanlık sonucu bir görünüşten diğer bir görünüş algılayabiliriz. Çoğu kez sıklıkla duyumsadığımız şeylerde, yerleşik bir alışkanlıkla, önyargı o kadar çabuk ve sürekli devreye girer ki duyumumuzun algısını yargımızla oluşturulmuş bir ide olarak ele alırız. Öyle ki, duyumla algıladığımız yalnızca diğerini ortaya çıkarmaya yarar ve pek dikkate de alınmaz; dikkatle anlayarak okuyan ya da dinleyen bir insan sesler ya da harflere değil de onlarla kendinde ortaya çıkan idelere dikkat eder çoğunlukla.”
23 John Locke, İnsan Anlığı Üzerine Bir Deneme, (çev. Vehbi Hacıkadiroğlu), Kabalcı Yayınevi, İstanbul, 1992, s. 112.
24 Locke bilişsel yaşamı, özbilinçli etmenlerde var olan yetiler varsayımı ile açıklıyor. Bu ve sonraki iki bölüm yetileri ve iç duyumumuzla edindiğimiz ideleri ele alırken yetileri yalın iç duyum idelerine bir tür ek olarak değerlendiriyor.
25 Burada çoğu çağdaşı gibi Locke da düşünce ve düşünmeyi şimdi yaygın olandan daha geniş bir anlamda kullanıyor.
26 John Locke, a.g.e. , s.113.
Şekil 6. Görsel algılama test örnekleri27
Yakın dönemde yapılan çalışmalarda obje tanımak için eğitilmiş derin yapay sinir ağlarının da insanlar gibi görsel illüzyonlara sahip oldukları belirlenmiştir.28 Obje tanımada insana yakın bazı durumlarda insandan üstün performans gösteren derin yapay sinir ağlarının neden görsel illüzyonlar algılıyor oldukları henüz yanıtlanmamıştır. Tahminlerden biri ise obje tanımak için bu görsel illüzyonların gerekli olabileceğidir. Yani insanı örnek alarak geliştirilen yapay sinir ağlarının insana benzer yanılgılara düşüyor olması ortak gerçekliğin sürdürülebilmesi için şartolabilir. Fakat J. Locke’un dikkat çektiği:
“...Çok erken yaşlarda edindiğimiz alışkanlıklar bizde önünde sonunda sıklıkla gözümüzden kaçacak eylemler yaratır... Zihnimizin kendi dış duyum idesini kendi yargı idesine dönüştürmesi ve birini, hiç dikkate almadan, diğerini ortaya çıkarmak için kullanmasında o kadar şaşılacak bir şey yoktur.”29
27 Görsel Kaynak : “Exploring Perceptual Illusions in Deep Neural Networks”, Journal of Vision, 2019.
28 Emily J. Ward, Exploring Perceptual Illusions in Deep Neural Networks, Department of Psychology, University of Wisconsin – Madison https://www.biorxiv.org/content/10.1101/687905v1.full 12 Aralık 2019.
29 John Locke, İnsanın Anlama Yetisi Üzerine Bir Deneme, Çev. Meral Delikara Topçu, Öteki Yayın Evi,2007, s.198. Ayrıca bkz. Patricia M. Churchland & Paul S. Churchland, “Could a Machine Think”, On the Contrary: Critical Essays, 1987-1997, Cambridge: MIT, s.51-60.
Locke’un işaret ettiği insan önyargılarının kullanımı ile ilgili durumların makineler için “gözümüzden kaçacak eylemler” yaratmadan nasıl engelleneceği üzerinde çalışılmalıdır. Çünkü güçlü yapay zekânın öngörülemez bir eylemde bulunmasının tahmin edilemeyecek büyüklükte zararlı etkileri olabilir.
Locke’un bahsettiği insandaki dış duyum idelerinin makine için veri setindenedinilen önyargı olduğunu düşünürsek bunun makinenin kendi yargı idesinden farklı olması ile birini hiç dikkate almadan diğerinin kullanılmasının engellenmesi için bu iki karar merkezinin bağımsız olması gerektiği düşüncesi ile makineler için etik kuralların oluşturulması çalışmaları ortaya çıkmıştır. Fakat bu etik kurallara göre programlanan bir makinenin temel aldığı yazılımın değiştirilemez kuralları güçlü yapay zeka söz konusu olduğunda değiştirilebilir olacaktır çünkü güçlü yapay zeka yani bilinç sahibi bir makinenin kendi donanımına ve yazılımına en yüksek seviyede hâkim olması beklenmektedir. Bu yüzden de güçlü yapay zekânın kendi yazılımı üzerinde değiştirilemez olarak programlanmış bir özelliği değiştirilebilir olarak tekrarprogramlaması mümkündür.
2014 yılında yayınlanan “Consciousness in the universe: A review of the ‘Orch OR’ theory”30 isimli makalelerinde Stuart Hameroff (1947- ) ve Roger Penrose (1931- ) Örgütlü Olarak Düzenlenmiş Nesnel İndirgeme (Orch-OR) teorisini ortaya attı. Buna göre nöronların içinde mikro tüpçük denilen protein sicimleri bulunmakta ve buyapıların içinde kuantum etkileşimleri oluşmaktadır. Örgütlü olarak düzenlenmiş nesnel indirgeme teorisine göre mikro tüpçükler içinde oluşan kuantum etkileşimleri sonucunda süper pozisyon ve dolanıklık hali çökerek çok sayıda olasılık tek bir değere indirgeniyor ve böylece insanların verdiği tekil kararlar ortaya çıkıyor. Buna göre Hameroff ve Penrose bilincin nöronları birbirine bağlayan sinaps, akson ve dendritlerde bulunan mikro tüpçüklerde ortaya çıktığını ve bunlar arasındaki karşılıklı etkileşimle şekillendiğini savunuyor.
30 Stuart Hameroff, Roger Penrose, "Consciousness in the universeA review of the ‘Orch OR’ theory", Physics of Life Rewiews, 2014, p.39-78. (Çeurimiçi) https://www.sciencedirect.com/science/article/pii/S1571064513001188?via%3Dihub, 12 Aralık 2019.
Nöroloji alanında yapılan son araştırmalar, beyindeki sinir ağının bir parçası olan dendritlerin hem kablo görevi görüp veri aktarımı yaptığını, hem de bilgisayarişlemcisi gibi çalışarak veri işliyor olduğunu gösterdi.31 Bu işlemlerin gerçekleştiği dendritlerin içindeki mikro tüpçükler Belirsizlik İlkesi’nin32 geçerli olacağı kadar küçük yapılardır. Bu da beyindeki bilgi işlem süreçlerinin kuantum fiziğinin etkili olduğu ölçeklerde gerçekleşebildiğini göstermektedir.
Makro boyutlarda ve yavaş cisimler üzerinde çalışan klasik fizikte bir parçacığın hızı ve konumu bilindiğinde o parçacığın geçmiş ve gelecekte nasıl hareket ettiği ya da edeceği hesaplanabilir. Atomik boyutlarda (kuantum düzeyi) ve ışık hızına yakın hızlardaki parçacıklar üzerinde çalışan modern fizikte ise belirlilik (determinizm) yoktur olaylar belli bir olasılıkla gerçekleşir.33 Yine de insan beyninde ortaya çıkan bu çok küçük ölçeklerde gözlemlenebilen kuantum etkileri, insan beyninin bir kuantum bilgisayar olduğunu söylemek için yeterli değildir. Roger Penrose insan beyninin standart kuantum bilgisayarlarda olduğu gibi elektromanyetik dolanıklıkla değil de yerçekimi etkisiyle çöken özel bir dolanıklık türüyle çalıştığını söyler.34 Henüz yerçekimi, kuantum fiziğiyle birleştirilerek hem makro hem mikro evrenlerde geçerli olabilecek bir ortak teori (string theory) ortaya çıkmadığı için bu iddianın şimdilik test edilmesi mümkün değildir. Fakat kuantum fiziğindeki ilerlemelerle ortak bir teori ortaya konulur ve bilincin fiziksel bir olgu olduğu gösterilebilirse ancak o zaman bilinç olgusunun da objektif bir zemine oturtulması mümkün olabilir.
31 Smith SL, Smith IT, Branco T, Häusser M., Dendritic spikes enhance stimulus selectivity in corticalneurons in vivo, Nature, 2013, p. 115-120. (Çevrimiçi)https://www.ncbi.nlm.nih.gov/pubmed/24162850, 12 Aralık 2019.
32 Belirsizlik ilkesi Werner Heisenberg tarafından 1927’de ortaya atılmıştır buna göre bir parçacığınhem konumu, hem momentumu ile ilgili eş zamanlı olarak kesin bilgiye sahip olmak mümkün değildir. Ayrıca bkz. David J Griffiths, Introduction to Quantum Mechanics, Pearson Prentice Hall, 2005.
33 Arthur Beiser, Çev. Gülsen Önengüt, Modern Fiziğin Kavramları, Akademi Yayınları, 2008, s. 125.
34 Roger Penrose, The Emperor's New Mind: Concerning Computers, Minds, and the Laws of Physics, Oxford University Press, 2016, s. 519.
2.4 Uzman Sistemler
Uzman Sistemler, yapay zekâ ile ilgilenen araştırmacılar sayesinde 1950’den beri gelişimi devam eden bir çalışma alanıdır. Bu süreçte araştırmacılar insandan daişlevli bir uzmanı, makineler sayesinde üretebileceklerine inanmışlardır. Fakat daha sonra, böyle bir yapılanma için henüz makinelerin donanımsal olarak yeterli olmadığı anlaşılmıştır. Bu inanç kapsamında oluşturulmaya çalışılan genel amaçlıprogramlardan yani insanın tüm özelliklerini gösterebilecek yetenekte olan programlardan, özel amaçlı programlara yani insanın belirli bir konudaki yeteneklerini taklit edebilen programlara geçiş 1960’ların ortalarından itibarengerçekleşmeye başlanmıştır.
1970’li yıllarda ise belirli bir alana yönelik uzman sistemler geliştirilmiştir. Busistemlerde bilginin merkezinin ne kadar önemli olduğunun farkına varan yapayzekâ araştırmacıları, uzman sistemlerin elde etmiş olduğu başarının onu oluşturmak için kullanılan uzmanının sınırlı bilgisinden kaynaklandığı sonucuna varmıştır. Uzman sistemler 1980’li yıllardan itibaren, akademiden ticarete geçmiş ve bu dönemde kullanıldıkları alanlar için özelleştirilmiş önemli programlar uygulamayakonulmuştur.35
35 Frank Puppe, Systematic Introduction to Expert Systems: Knowledge Representations and Problem-Solving Methods, Springer Science & Business Media, 2012, s.7-14
Uzman Sistemlerin ilk kullanım alanları arasında sağlığa ilişkin uygulamaların yer aldığını görürüz. Bu alanda görülen başarı ile güvenlik, askeriye, bankacılık gibi diğer alanlarda da kullanımı için çalışmalar yapılmıştır. Bu uygulamaların çalışma mantığı; bilgilerin veri tabanlarına depolanması ve daha sonrasında benzerproblemlerle karşılaşıldığında bu veri tabanlarının üzerinde yapılan çıkarımlarla sonuçlara ulaşılması şeklindedir. Bu özellikleriyle uzman sistemler uzmanlık gerektiren sorunları çözmek için uzmandan alınan bilgilerin depolandığı bilgisayarlardaki bilgiyi kullanan sistemlerdir.
Şekil 7. Uzman Sistemin Çalışma Algoritması
İlk uzman sistemlerden biri olan MYCIN, 1970 yılında Stanford Üniversitesi’nde Edward Feingbaum ve ekibi tarafınca oluşturulmuştur. Bakteriyolojik ve menenjitik gibi hastalıkların teşhisi ve uygun yöntemleri önererek tedavisinin sağlanması için çalışan bir sistemdir.
Sisteme girilen veriler; laboratuar sonuçları, hastanın geçirdiği hastalıklarınbilgileri, sahip olunan semptomlardır. Girilen bu bilgiler değerlendirilir ve çıktısı; reçete yazımı, teşhis koyma, tedavi süreçlerinin belirlenmesi olarak alınır.
Böylece MYCIN’in teşhisi ve uygun bulduğu tedavi şekli doktora bildirilir. MYCIN sorgulandığında ise verdiği kararlar hakkında açıklamalar yapabilmektedir.
MYCIN'in uzman hekimle karşılaştırıldığında bakteriemi ve menenjit tedavisinde daha başarılı olduğu gözlenmiştir, buna rağmen MYCIN hiçbir zaman kullanıma açılmamıştır. Buna neden olarak etik sorunlar, -örneğin hata yapılırsa bundan kimin sorumlu olacağı gibi nedenler- gösterilmiştir.36
36 Thomas D. McFarland-Reese Parkers, Expert Systems in Education and Training, Educational Technology, 1990, s.26-33.
Ayrıca Bkz. (Çevrimiçi) http://www.aaai.org/Papers/Buchanan/Buchanan03.pdf ,http://www.aaaipress.org/Classic/Buchanan/buchanan.html 12 Aralık 2019.
ÜÇÜNCÜ BÖLÜM
MAKİNE ÖĞRENMESİ
Turing, Hesaplama Makineleri ve Zekâ isimli makalesinin son bölümü olan Öğrenme Makinesi’nde (Learning Machine) taklit oyununu başarıyla oynayabilecek, öğrenen bir makinenin gereklilikleri hakkındaki görüşlerini ifade eder. Turing yetişkin bir insanı taklit etmeye çalışırken, yetişkin zihninin bugünkü durumunda olmasına yol açan süreçleri göz önünde bulundurmanın önemli olduğunu belirtir vebu süreçleri şu şekilde sınıflandırır:
1. Zihnin ilk hali, buna doğum anındaki hali denebilir,
2. Doğumdan sonraki süreçte almış olduğu eğitim,
3. Almış olduğu eğitim dışında kazandığı deneyimler.1
Turing, çocuk zihni için tüm bu süreçler göz önüne alındığında, çocuğun zihnini simule eden bir programın yetişkin zihnini simule eden bir programa göre dahakolay oluşturulabileceğini söyler. Bu durumda iki sorun ortaya çıkar: çocuk zihninin simule edilmesi ve çocuk zihninin eğitim süreci. Turing’e göre ödül ve ceza yöntemini içeren bir öğrenme süreci, zihinde oluşması istenen kalıpları seçecek özellikte olmalıdır. Turing, tüm bu süreci şu bakımlardan evrim sürecine benzetir:
Çocuk makinenin yapısı = Kalıtsal malzeme
Çocuk makinedeki değişiklikler = Mutasyon,
Doğal seçilim = Deneycinin yargısı2
1 Alan M. Turing, Computing Machinery and Intelligence, s.452.
2 Alan M. Turing, a.y.
Ayrıca bu sürecin bilgisayarlar için insan evriminden daha hızlı gerçekleşebileceğini de ekler çünkü O’na göre en uygun olanın hayatta kalması, var olan avantajları ölçmek için yavaş bir yöntemdir.3 Yani Turing’e göre insan beyni mekanik bir şekilde işlemektedir ve doğal seçilim bu mekanik yapının sahip olduğu avantajları ölçmek için çok yavaş bir yöntemdir. Fakat bu yöntemi makineler üzerinde simule edebilir dolayısıyla hızlı bir yapay seçilim oluşturabiliriz. Bunun sağlanması için de öncelikle beyinde gerçekleşen en temel fonksiyon olan ‘öğrenme’yi, makinelere öğretmemiz gerekir. Bu noktada öğrenmeyi, kısaca deneyimlerden çıkarım yapmak olarak tanımlayabiliriz. İnsanlar yeni bir durumla karşılaştığında bunu sıfırdan değerlendirmek yerine geçmiş deneyimlerinden edinilen bilgiler (alınan eğitimden ya da günlük hayattaki deneyimlerden elde edilen bilgiler) ışığında değerlendirirler ve buna göre bir çıkarım yaparlar. İlk defa karşılaşılan bir durum geçmiştekilere benzetilerek yorumlanmaya ve buna göre uygun eylem (tepki) bulunmaya çalışılır. Makinelerin öğrenmesi için de insana özgü olan bu durum örnek alınmıştır. Makine öğrenmesi araştırmalarının amaçları arasında; geçmişteki verileri kullanarak yeni bilgiler ortaya koymak ve bu bilgileri makinelerin davranışlarına yansıtmak ya da gelecek için doğru tahminlerde bulunmak vardır. Buna göre makine öğrenmesi, öğrenebilen ve kendisine aktarılan veriler üzerinden tahminde bulunan algoritmaları oluşturmaya yönelik çalışmalarıkapsar.4 Buna göre makine öğrenimi, bilgisayara detaylı ve doğru komutlar verdiğimiz geleneksel programlamadan farklıdır; temel olarak bir sistem oluşturup bu sistemin tutarlılığını veri ile desteklemek ile ilgilidir.
Makine öğrenmesi algoritmaları bilgisayarların, örnek veri kümeleri üzerinde eğitilmelerini ve belli aralıktaki değerleri belirlemek için istatistiksel analiz yöntemlerini kullanmalarını sağlar.5 Bu yöntemler sayesinde belli aralıktaki değerlerden oluşan bir kalıp (model) oluşturulur. Bu kalıplara karşılık gelen etiketlersayesinde önce öğrenme, daha sonra (benzer durumla karşılaştığında) deneyimlerden yararlanarak çıkarım yapma ve buna bağlı olarak karar alma sağlanır. Geleneksel programlama ve makine öğrenmesi kavramlarını daha iyi açıklayabilmek için algoritma ve optimizasyon gibi kavramların tanımlarına yer vereceğiz.
3 Alan M. Turing, a.g.e. , s.453.
4 Jesus Salcedo, Machine Learning for Data Mining, Packt Publishing, 2019, s. 5.
5 Ethem Alpaydın, Introduction to Machine Learning, London: The MIT Press, 2004, s.14.
3.1 Algoritma ve Hesaplamalar
Makine öğrenmesinin herhangi bir probleme çözüm sunabilmesi için problemin mantıksal ve matematiksel düzlemde ifade edilebilir olması yeterlidir. Çünkü bir problemin makine tarafından çözümlenebilmesi için öncelikli şartmantıksal ve matematiksel olarak ifade edilebilir olmasıdır, böyle bir çözümleme içinuygulanacak olan işlem dizisine de algoritma denir.6 Bilgisayar bilimlerinde tüm programlama dillerinin temelinde algoritma vardır. Bu yüzden bir makineyi programlamanın en önemli kısmı belirli bir problemin çözümü için algoritma hazırlayabilmektir. Algoritmanın oluşabilmesi için gerekli şartlar şu şekildedir:
. Her adımda ne yapılacağı en net haliyle ifade edilmelidir.
. Belirli sayıda işlem yapıldıktan sonra algoritma tamamlanmış olmalıdır.
. Algoritma herhangi bir problemle ilgili ortaya çıkabilecek tüm ihtimalleri ele alabilecek kadar genelleştirilmiş bir yapıda olmalıdır. (tüm girdiler/değişkenler(variable) için ortak çözüm)7
6 Ibrahim (Abe) M. Elfadel, Duane S. Boning, Xin Li, Machine Learning in VLSI Computer-Aided Design, Springer, 2019, s. 234.
7 Alexander Shen, Algorithms and Programming: Problems and Solutions, Springer Science & Business Media, 2011, s.70.
Bilgisayar programında bir algoritmanın çalışabilmesi için gerekli olan tüm girdiler “değişken” (variable) olarak isimlendirilir. Algoritmanın içindeki döngüler ve yapılan işlemler, bu değişkenlerin değerleri üzerinden gerçekleşir.
Şekil 6. Görsel algılama test örnekleri27
Şekil 6’da görülen, otonom bir aracın sensöründan gelen veri girişi ile oluşturulmuş bir algoritma örneğidir. Bu araç 15 cm mesafe boyunca önünde bir engel olup olmadığını kontrol etmekte ve eğer engel yoksa ilerlemekte herhangi bir engelle karşılaşmışsa sağa dönmektedir. Bu işlem sonsuza kadar devam etmektedir.
Şekil 8 . Otonom bir araç için oluşturulmuş hareket algoritması.
3.1.2 Optimizasyon ve Minimax Algoritması
Yukarıda belirttiğimiz gibi makine öğrenmesinde, makinelerin örnek veri kümeleri üzerinde eğitilmeleri ve belli aralıktaki değerleri belirleyebilmeleri içinistatistiksel analiz yöntemi olan optimizasyon kullanılır. Genel olarak, eldekikaynaklar bağlamında en uygunu (optimumu) bulma yöntemi olarak tanımlayabileceğimiz optimizasyon, klasik istatistik tekniklerinin yetersiz kaldığıdurumlarda yapay zekâ ile yeni çözüm yolları bulmuştur.8 Yapay zekâ tabanlıoptimizasyon teknikleri, çeşitli mantıksal ve matematiksel çözüm yaklaşımları çerçevesinde şekillenen algoritmalar olarak bilinmektedir.
8 Suvrit Sra, Sebastian Nowozin, Stephen J. Wright, Optimization for Machine Learning, MIT Press, 2012, s.2.
1950'lerde algoritmaları kullanabilecek gelişmişlikte ilk bilgisayarlar üretildiğinde, en belirgin yapay zekâ problemleri oyunlardı. Çünkü oyunlar, kâr ya dazararın kolay ölçülebilirliği, basit kuralları ve çok sayıda denklem içeren hamle olasılıklarının olması nedeniyle ideal bir örneklem alanı oluşturmaktadır. Şans faktörünün olmadığı, taktik, hesaplama, strateji ve bilgi birikimine dayalı olan oyunlar için geliştirilen bilgisayarlar, yapay zekâya ihtiyaç duyulan oyun dışındaki problemlere de kolayca uyarlanabilirler. Bu nedenle dama, satranç ve GO9 gibi tahta oyunları güncel yapay zekâ araştırmalarının da konusu olmuştur.
Bir oyuncunun kaybının başka bir oyuncunun kazancı olduğu sıfır toplamlı oyunlarda ise karar vermek için genellikle minimax algoritması kullanılır. Bu oyunlarda en doğru hamlenin yapılmasını hedefleyen minimax ağacı; kaybı en aza indirmek (minimize etmeye) ve kazancı en yükseğe çıkarmak (maximize etmeye) için oluşturulur. 10
9 Dünyanın en eski zekâ ve strateji oyunu olma özelliği taşıyan Go oyununu 19×19’luk bir alanda 180 beyaz 181 siyah taşla oynanır ve tüm taşlar eşittir(hiyerarşi yoktur). Oynanabilecek hamle olasılıkları çok yüksektir. Google DeepMind şirketinin geliştirdiği AlphaGo isimli yapay zekâ uygulaması Mart2016’da 18 kez Dünya Go Şampiyonu olmuş Lee Sedol’u 5 maçlık bir seride 4-1 yenmiştir.
10 Stuart J. Russell, Stuart Jonathan Russell, Peter Norvig, Ernest Davis, Artificial Intelligence: A Modern Approach, Prentice Hall, 2010, s. 165.
Tic-tac-toe oyunuyla örneklendireceğimiz gibi minimax ağacı, her düğümde (node) farklı durumlar için olasılık değerlerini hesaplar. Bu hesaplara göre sondüğümden yukarıya doğru en yüksek değerleri seçer ve böylece bütün ağaçtaki en doğru seçenek seçilmiş olur. (Bkz. Şekil 8)
3.1.3 Tic Tac Toe Oyunu ve Karar Ağacı (Minimax Algoritması)
Tic Tac Toe oynanan 3×3 bir tabloya sırasıyla X ve O işaretlerinin konulduğu bir oyunda, Şekil 9’daki gibi bir karar ağacı çıkarılabilir.
Şekil 9. Mevcut durum için Tic-tac-toe oyununda Minimax Karar Ağacı11
Bu karar ağacında ağacın kökünü (root) oluşturan ilk durumdan itibarenoyuncular sırayla hamle yapmaya devam ettiğinde oyunun hangi olasılıkları barındırdığı görülmektedir. İkinci sırada karar verecek taraf olan ve tahtaya X sembolünü yazan oyuncunun oynayabileceği tüm olasılıklar toplamı 3’tür ve buolasılıklar karar ağacında birer alt düğüm olarak yer alır. Bir alt seviyede ise X’in oynanabileceği tüm durumlarda, O işaretinin yazılabileceği olasılıklar toplamı 6 tanedir.
Bir minimax ağacının hesaplanması sırasında kaç adım gidileceği ise ağacınseviyesini gösterir. Buna göre ilk şekildeki minimax ağacı iki seviyeli, X’in son hamlesi için hesaplanacak olan son karar ağacı ise üç seviyeden oluşan bir ağaçtır.
Bir minimax karar ağacının seviyesinin yüksek olması alınan sonucun seviyedeğerine göre yüksek olasılıkla doğru bulunmasını sağlar ve bu da yapay zekânın başarısını arttırır.12 Daha yüksek seviyeli karar ağaçları kurmak için daha yüksek hafızaya (RAM) sahip bilgisayarlar gereklidir. Henüz çok yüksek kapasiteli sistemler mevcut olmadığı için GO gibi hamle olasılıklarının yüksek olduğu oyunlarda, hafızanın yetersiz olabileceği ihtimaline karşı, bu karar ağacı seviyesi belirli bir limitin altında tutulur.
11Şekil kaynak: Bilgisayar Kavramları- Şadi Evren Şeker (Çevrimiçi):http://bilgisayarkavramlari.sadievrenseker.com/2009/04/29/minimax-agaclari-minimaxtree/ 12Aralık 2019.
12 A.e. , s. 670.
Son olarak bilgisayarın karar verebilmesi için her hamleye sayısal bir değer oluşturabilmek ve aşağıdaki gibi her hamle durumunu puanlamamız gerekir.
Şekil 10. “O” nun hamlesi için alınmış değerler
Yukarıdaki karar ağacına göre ilk durum için; 1 puanındaki hamleyi yapması durumunda X her koşul altında oyunu kazanmaktadır.
3.2 Makine Öğrenmesi Yöntemleri
Makine öğrenmesi yöntemleri ise gözetimli (supervised) ve gözetimsiz (unsupervised) öğrenme olarak iki ana başlıkta incelenir. Bunlar arasındaki temel fark öğrenilen bilginin gelişen sisteme nasıl aktarıldığıdır.
3.2.1 Gözetimli ve Gözetimsiz Öğrenme
Gözetimli öğrenme yönteminde, veriler insanlar tarafından, beklenen çıktıları işaret edecek şekilde etiketlenerek sisteme aktarılır. Daha sonra ise karşılaşılan etiketsiz veriler üzerindeki etiket değerlerini tahmin etmek için modeller kullanır. Buna göre çıktıyı öğrenen makine, beklenen ve gerçekleşen arasındaki farka yol açan hatayı göz önüne alarak oluşturmuş olduğu modeli günceller. Gözetimsiz öğrenmede ise bir veriyi etiketleme işlemi uygulanmaz. Belirli bir doğru işaret edilmeden karmaşık bir veri kümesinden bazı şablonlar çıkarılır. Örneğin, gözetimli öğrenme ile bilgisayara hangi verilerin kedi resimleri içerdiği tek tek verileri etiketleyerek öğretilirken, gözetimsiz öğrenmede sistemin kedi resimlerinin ortaközelliklerini belirlemesi sağlanır. 13
Şekil 11. Makine öğrenmesi yöntemleri14
13 Ethem Alpaydın, Introduction to Machine Learning, London: The MIT Press, 2004, s.4.
14 A.e.
Bazı durumlarda çözülmesi gereken problem makine öğrenmesi için çok zor olabilir ve genellikle doğru etiketi üreten mükemmel bir yöntem elde edilemez. Böyle durumlarda, iyi fakat mükemmel olmayan bir tahmin hiç olmamasından daha iyi olabilir. Bazen insanlar olarak böyle durumlar için -makine kullanmadan- daha iyi tahminler üretebiliriz, ancak yine de makine öğrenmesini kullanmayı tercih edebiliriz çünkü makine tahminlerini daha hızlı yapacaktır ve yorulmadan tahminlere devam edecektir. Büyük veriler söz konusu olduğunda, makinelerin insanlardan daha iyi olduğu alanlara örnek olarak: hangi müziğin, hangi videoların veya hangi reklamların hangi kullanıcı için daha fazla ilgi çekici olacağını tahmin eden öneri sistemleri gösterilebilir.
Gözetimli öğrenmede ihtiyaç duyulan doğru bir şekilde etiketlenmiş veri kümelerinin oluşturulması kolay bir işlem değildir. Bazen de araştırmacılar, cevaplarını bilmedikleri ancak elde etmiş oldukları verinin içinden ayrıştırılabilecek sorular sorarlar. Gözetimsiz öğrenmeye ihtiyaç duyulan nokta burasıdır.
Gözetimsiz öğrenmede, bir öğrenme modeline, onunla ne yapacağına dair açık talimatlar olmadan bir veri seti verilir. Eğitim veri seti, istenen bir sonucu veya doğru bir cevabı olmayan bir örnek koleksiyonudur. Eldeki soruna bağlı olarak, gözetimsiz öğrenme modeli, verileri farklı şekillerde düzenleyebilir.15
15 Michael W. Berry, Azlinah Mohamed, Bee Wah Yap, Supervised and Unsupervised Learning for Data Science, Springer Nature, 2019, s.4.
3.3 Derin Öğrenme
Derin öğrenme, matematik, bilgisayar bilimi ve sinir bilimde kökleri olan bir makine öğrenim dalıdır. Diğer makine öğrenmesi tekniklerinden farklı olarak tek birkatmanda değil, çok katmanlı yapılarla hesaplamaları tek bir seferde yapar ve diğer yöntemlerde tanımlanması gereken parametreleri derin öğrenme veri üzerindenkendisi keşfedebilir.16 1950'lerde yapay zekânın nasıl yaratılacağına dair iki rakip görüş vardı bunlardan biri mantık ve klasik bilgisayar programlarına dayanıyordu; diğeri doğrudan veriden öğrenmeye dayanıyordu. Doğrudan veriden öğrenme yöntemi olan derin öğrenmenin olgunlaşması mantık ve klasik programlamanın gelişimi göz önünde bulundurulduğunda çok daha uzun sürdü. Yirminci yüzyılda, bilgisayarların işlemcilerinin yeterince güçlü olmadığı ve veri depolamanın günümüz standartları ile karşılaştırıldığında yetersiz olduğu durumlarda, klasik programlama sorunları çözmek için etkili bir yoldu. Programcılar her problem için farklı bir program yazıyordu ve problem ne kadar büyükse program o kadar büyük oluyordu.Günümüzde ise işlemciler daha güçlü hale gelmiş ve veri miktarı artmış durumda bu yüzden öğrenme algoritmalarını kullanarak derin öğrenme ile sorunları çözmek daha hızlı, daha doğru ve daha verimli bir yöntem.17
16 Terrence J. Sejnowski, The Deep Learning Revolution, The MIT Press Cambridge, 2018, s.3.
17 A.e.
3.3.1 Yapay Sinir Ağları
Yapay sinir ağları beyin hücrelerinde gerçekleşen öğrenme yapısının taklit edilmesi (matematiksel olarak modellenmesi) üzerine kurulu yapay öğrenme tekniğidir. Bilindiği kadarıyla biyolojik sinir sisteminde hiyerarşik bir elektriksel akımsonucu algılama gerçekleşmektedir. Benzer olarak yapay sinir ağı da hesaplamalarlatekrar tekrar değişebilen elektriksel akımlarla şekillenir.18 Bu açıdan incelediğimizde sinir ağının kendisi bir algoritma değil, farklı öğrenme algoritmalarının birlikte çalışması ve karmaşık veri girişlerini işleyebilmesini sağlayan bir çerçevedir. Temeldebir yapay sinir ağında yapılan matematiksel işlemler; giriş değerleri ile ağırlık değerlerinin çarpılması, önyargıların eklenmesi (bias) ve aktivasyon fonksiyonununuygulanması olarak özetlenebilir.
18 Graupe Daniel, Principles Of Artificial Neural Networks: Basic Designs To Deep Learning, World Scientific, 2019, s.1.
Şekil 12 Matematiksel nöron modeli; bir sinir hücresinin birden fazla girdiyi alarak bir çıktı üretmesi prensibine dayanır.19
19 Görsel Kaynak: Stanford University, CS231n: Convolutional Neural Networks for Visual Recognition,http://cs231n.stanford.edu/slides/2019/cs231n_2019_lecture04.pdf, 12 Aralık 2019.
3.3.1.1 İlk Yapay Sinir Ağı Mimarisi
Yapay sinir ağı mimarisi alanında yapılan ilk çalışma 1943 yılında, matematikçi Walter Pitts (1923-1969) ve nörofizyolog Warren McCulloch (1898-1969) tarafından yayınlanan Sinir Etkinliğinde Bulunan Fikirlerin Mantıksal Bir Hesaplaması20 isimli makalede ortaya konulmuştur. McCulloch ve Pitts bu makale ile canlı beyninde yer alan biyolojik nöronların, birlikte nasıl çalıştıklarının indirgenmiş bir modelini göstermişlerdir. Makalelerinde McCulloch ve Pitts, bu yapay nöronlar ile oluşturulan yapay sinir ağlarının, ifade edilebilen herhangi bir mantıksal önermeyi hesaplayabileceğini de göstermişlerdir.21
20 Walter Pitts- Warren McCulloch, A Logical Calculus of Ideas Immanent in Nervous Activity, 1943(Çevrimiçi) https://www.cs.cmu.edu/~./epxing/Class/10715/reading/McCulloch.and.Pitts.pdf, 12Aralık 2019.
22 James A. Anderson- Edward Rosenfeld,Talking Nets: An Oral History of Neural Networks, Bradford Book, 2014, s.3-15.
McCulloch beyni modellemeye çalışırken Russell ve Whitehead'in yazdığı ve bütün matematiğin sadece temel mantık kullanılarak kurgulanabileceğini göstermeye çalıştığı Principia Mathematica kitabından ilham almıştır.22 Principia Mathematica kitabında en temel parça önermedir mümkün olan en basit ifade ise doğru ya da yanlıştır. Önermelerle daha karmaşık ağlar oluşturmak için ise ve, veya ve değil gibi temel mantıksal işlemler kullanılmıştır. Russell ve Whitehead bu basit önermelerden, modern matematiğin tüm karmaşıklığını türetmeyi denemişlerdir. McCulloch bu modeli, bir matematikçi olan Pitts’e anlatmış ve makalelerinde bu yapay sinir ağı modelinin matematiksel bir ifadesini oluşturmuşlardır. Böylece yapay bir sinir hücresi sayesinde her türlü mantıksal ifadenin formülize edilmesinin mümkün olabildiğini göstermişlerdir.
Şekil 13 Mantıksal önermeler ve nöronlar arasındaki bağlantılar
3.3.1.2 Tek Katmanlı Algılayıcı
Nöropsikolog Donald Hebb (1904-1985) 1949 yılında “The Organization of Behavior” isimli makalesinde, “Bir biyolojik nöron başka bir nöronu tetiklediğinde, iki nöron arasındaki bağlantı güçlenmektedir” fikrini ortaya atmıştır.23 Bu fikir daha sonra Hebb Kuralı olarak adlandırılmıştır. Perceptron kavramı ise ilk olarak 1957 yılında Cornell Üniversitesi’nde psikolog olan Frank Rosenblatt (1928-1971)tarafından ortaya konulmuştur. Hebb Kuralı dikkate alınarak eğitimi gerçekleştirilen perceptron tek bir yapay sinir hücresinden oluşmaktadırlar.24
23 Donald Hebb, The Organization of Behavior, Psychology Press, 1949.
24 Frank Rosenblatt, The Perceptron A Perceiving And Recognizing Automaton,1957. (Çevrimiçi)https://blogs.umass.edu/brain-wars/files/2016/03/rosenblatt-1957.pdf, 12 Aralık 2019. Ayrıca bkz. (Çevrimiçi) http://nautil.us/issue/21/information/the-man-who-tried-to-redeem-the-world-with- logic, 12 Aralık 2019.
Perceptron, giriş/çıkış ünitelerinden oluşur ve bir doğrusal eşik biriminesahiptir. Eşik değeri probleme göre belirlenir ve bu eşik değeri kullanılarak veri seti üzerinde bir sınıflandırma yapılır. Perceptron gibi Hebb öğrenme kuralı kullanılanyapay sinir ağı modellerinde temel amaç yapay nöronlar arasındaki bağlantıların ağırlık değerlerinin, değişebilen değerleri olan parametreler ile kayıtlı tutulması ve bu parametrelerin, üzerinde çalışılan veri işlendikçe değişerek en uygun değere ulaşmasıdır.
Perceptron, aynı zamanda Frank Rosenblatt tarafından 1957 yılında geliştirilenbir makinenin ismidir. Görüntü tanıma için geliştirilen bu makine, 400 tane fotoselin,yapay nöronlara rastgele bağlanması ile oluşturulmuştur. Bu 400 fotosel aracılığıyla algılanan ışık sinyalleri ve ağırlık değerleri üzerinden yapılan hesaplamalarsonucunda Perceptron 1 ya da 0 çıktısı üretir. Yani, farklı görseller ile eğitilerek ağırlık değerleri değiştirilen Perceptron, eğitimin sonunda gösterilen görselin iki gruptan hangisine ait olduğunu belirtebilir seviyeye gelmiştir.25
25 Frank Rosenblatt, a.e.
3.3.1.3 Yapay Sinir Ağları Nasıl Öğrenir?
Yapay sinir ağlarını telli bir çalgı aleti olarak düşünürsek, eğitim verileriyle eğitilmiş bir sinir ağını akordu yapılmış bir müzik aletine benzetebiliriz. Akort sürecinde izlenen yöntem; teller arasındaki uyumu yakalamak için notaya tekrar tekrar basmayı, her seferinde hataları azaltmayı ve sonunda makul şekilde ayarlanmış bir çalgı aletine ulaşmayı sağlar. Yapay bir sinir ağında bu şekilde uygunbir ayarlama elde etmek için eğitimi gerçekleştiren her yinelemede, beklenen değere ulaşabilmek için geri yayılım (backpropagation) uygulanır böylece ağ eğitilir ve böylece düşük hata oranlarına sahip çıktılar üretebilir.26
26 Graupe Daniel, Principles Of Artificial Neural Networks: Basic Designs To Deep Learning, World Scientific, 2019, s.22.
Bir sinir ağı, her biri kendi içinde hesaplamalar yapan birçok nörondan oluşur. Tek bir nöron, kendisine bağlı sinaptik ağırlıklar (synaptic weights) olarak adlandırılan bir değerler dizisine sahiptir. Bu ağırlıklar sinir ağı eğitildikçe eğitim verilerindeki değerler doğrultusunda değişmektedir. Yapay sinir ağlarında öğrenmenin nasıl gerçekleştiğini açıklayabilmek için Python programlama dilinde yazılmış aşağıdaki kod örneğini ele alacağız.
Örneğimizin odağı, bir sinir ağı oluşturmak, onu 10000 tekrar ile eğitmek, hertekrarda çıktısını tahmin etmek, beklenen çıktı değeri ile karşılaştırarak hatayı elde etmek, hatayı temel alarak ağırlığı ayarlamak/güncellemek ve son olarak test için eğitim verilerinden farklı bir girdi vererek çıktıyı tahmin etmek olacaktır.
İnceleyeceğimiz örnekte çok basit bir eğitim veri seti kullanacağız, bu sette 3 ikili değer ve bir çıktı değeri var:
Bu veri setinde girdi dizisindeki ilk değer neyse çıktı değerinin de aynı değere eşit olduğu örüntüsünü görebiliyoruz. Sinir ağının eğitimi tamamlandığında bu örüntüyü herhangi bir girdi üzerinde de tanıyabiliyor olması beklenir. Örneğin, [1, 1, 0] girdisi için eğitim verileri ile oluşturulmuş olan modele göre vereceği çıktı 1’e çok yakın bir değerdir.
Örneğimizde Python’da matematiksel işlemler için kullanılan Numpy kütüphanesini kullanıyoruz öncelikle “import” komutuyla bu kütüphaneyi programımıza ekliyoruz sonrasında eğitim veri setimizi “input” ve “output” olarak iki ayrı dizi şeklinde oluşturuyoruz. Matris çarpımı işlemi için “T” (transpose) fonksiyonu ile “training_set_outputs” matrisini yataydan dikey hale getiriyoruz.
Burada gördüğümüz “random()” rastgele sayılar üreten bir fonksiyondur. “seed()” fonksiyonu ise eğitime her başlandığında aynı rastgele ağırlık değerlerini alabilmeyi sağlar. Bu sayede eğitime sıfırdan başlandığında, model aynı rastgele başlangıç ağırlıkları grubuna getirilebilir böylece model tekrarlanabilir bir hale gelir bu da yapılan değişikliklerin ya da ortaya çıkan hataların kolaylıkla gözlemlenebilmesini sağlar. Rastgelelik derin öğrenme için önemli bir konudur bu yüzden koddaki bu fonksiyonu biraz ayrıntılı inceleyebiliriz. Bilgisayarda rastgele sayı üretimi aslında bildiğimiz anlamıyla "rastgele" değildir. Programlama yoluyla üretilen rastgele sayılar deterministliktir ve ürettiği dizi random.seed(x) fonksiyonuna atadığımız tohum değerini (x) referans alarak belirlenebilir. Bunagöre, aynı tohum değerini iki kez verirsek, aynı rastgele sayı dizisini iki kez elde edebiliriz. Dolayısıyla, bilgisayarda rastgele bir sayı üretmek, algoritmalar üzerinde çalışıldığı için aslında rastgele değildir. Algoritmalar her zaman aynı girişi temel aldığında aynı çıktıyı verir. Genelde “daha rastgele” sayı dizileri üretebilmek için “zaman” otomatik olarak seed() fonksiyonuna atanır ancak burada da makinenin dikkate aldığı zamansal değeri tekrar verdiğimizde tekrar aynı değere ulaşabilme imkânı vardır.
Örneğimize geri dönersek başlangıç için rastgele oluşturduğumuz ağırlık değerleri eğitim verilerimizle tutarlı olması için 3x1 matris boyutlarındadır. Eğitim verilerinin 3x1 matris boyutlarında olmasının nedeni ise şekilde görüldüğü gibi 3 girdisi (input) 1 çıktısı (output) olan bir yapay nöron modellemekte olmamızdır. Ayrıca ağırlık değerlerini -1 ile 1 arasındaki rastgele sayılardan üretmemiz gerekir çünkü çıktı değerlerimiz 0 veya 1'dir. a - b aralığı için “random” fonksiyonu kullanılırken, fonksiyon şöyle tanımlanır: (b - a) * random_sample () + a,örneğimizde a = -1 ve b = 1 olur ve denklem burada şu değerleri alır:synaptic_weights = 2 * random.random ((3, 1)) - 1. Ağırlıkların değerleri pozitif, negatif veya sıfır olabilir.
Daha sonra bu rastgele ağırlık değerlerini normalleştirmek (normalization) yani işlemlerimizde işe yarar hale getirmek/makul değerler almasını sağlamak için sigmoid aktivasyon fonksiyonunu kullanacağız. Sigmoid fonksiyonu ile girdilerin ağırlıklı toplamı 0 ile 1 arasında normalleşir. Sigmoid fonksiyonunun türevi bu sigmoid eğrisinin gradyanıdır. “gradyan” veya “sigmoid türevi” bize herhangi bir noktada eğriye çizilen teğetin eğimini verir, bu da hatadan ne kadar uzak olduğumuzu anlamamıza yardımcı olur. Bu nöral ağı telli bir müzik enstrümanı olarak düşündüğümüzde grandyan değeri akort işlemi sırasında bize belirli bir nota ile ne kadar uyumsuz olduğumuzu söyler. Sigmoid fonksiyonunu aşağıdaki gibi tanımlayıp kullanabilirdik fakat biz daha kısa ve anlaşılır olacağını düşündüğümüz için işlemlerin içine gömerek kullanmayı tercih ediyoruz.
Burada eğitim için “for” döngüsü ile 10000 tekrarlama yapacağımızı söylüyoruz. Ağı eğitmek için çok fazla tekrar yapılırsa “overfit” olarak bilinen fazla uyum sorunu ortaya çıkmaktadır bu da bilgisayarın “ezberci” diye tanımlanan bir davranış sergilemesi demektir. Gerekli olan yineleme sayısı genellikle eğitimverilerinin boyutlarına ve probleme göre belirlenir.
Burada döngünün içinde yapılan işlemler; öncelikle çıktıya (output) yapılan atama ile başlamaktadır. Yukarıda verdiğimiz sigmoid fonksiyonunun tanımı içindeki “x” yerine girdi (input) ve sinaptik ağırlıkların (synaptic_weights) matris çarpımının değerini yazıyoruz. Böylece eğitim verilerindeki girdiler (training_set_inputs) ve ağırlık değerlerini (synaptic_weights) matris çarpımı yapan “dot” işlemine alıyoruz ve burada elde edilen çarpım değerlerini sigmoid fonksiyon içinde kullanıyoruz. Sigmoid fonksiyonu çıktıyı tahmin etmek için, sinir ağlarında kullanılan yaygın bir yöntemdir. Matris çarpımı ile elde edilen sonucun 0 ve 1 arasında bir değer almasını yani “normalleştirilmesini” sağlar.
(training_set_outputs - output) işlemi ile eğitim verilerindekiçıktılardan, sigmoid fonksiyonu ile elde edilen tahmini çıktı değerleri çıkarılarak hata (error) değeri bulunur. Gradyan hesabının yapıldığı kısım ise (output * (1 – output )) işleminin yapıldığı yerdir.
Bu son satırda özetle, çıktı değerlerini değiştirmek için hata değeri yani “training_set_outputs – output ” işleminin sonucu sigmoid fonksiyonun gradyanı ile çarpılır ve bunların matris çarpımı için eğitim girdilerinin (train_input) transpoze (.T) değeri alınır. Döngü her çalıştığında son adımda, synaptic_weights değerine, bu işlemlerden elde edilen değeri ekleyerek güncellemektir.
Eğitimi tamamlandıktan sonra test için girdi olarak [1,0,0] dizisini verdiğimizde 1’e çok yakın bir değer olan 0.99993704 değerini elde ettik.
Eğitim verilerini çoğunluğu 0 ile başlayacak şekilde değiştirdiğimizde ve 0 ile başlayan bir test dizisi girdiğimizde çıktı değeri bu kez 0’a çok yakın bir değer olarak 0.00224634 değerini almıştır.
Kodlama alanında bu yaklaşımla, yazılımın desenler için belirli kuralları kodlamak zorunda kalmadan faydalı bir tahmin üretmesi sağlanmaktadır.
Klasik programlamayla bu örneği ele aldığımızda yukarıdaki kodu dayazabilirdik. Burada dizideki ilk rakam “1” ise “1” yaz aksi durumda “0” yazdır demiş oluyoruz. Fakat büyük veri setleri söz konusu olduğunda bu yöntemin hiçbir işlevselliği yoktur.
3.3.2 Çok Katmanlı Yapay Sinir Ağları
XOR problemi27 ile birlikte tek katmanlı olan Perceptron modeli 1969 yılına gelindiğinde üzerindeki ilgiyi kaybetmiştir. Marvin Minsky (1927-2016) ve Seymour Papert (1928-2016) perceptron’un tüm limitlerini ele alan çalışmalarında28; tekkatmanlı perceptron’un basit problemler için geçerli iken, XOR problemi gibi problemlerde çözümden uzaklaştıklarını göstermişlerdir.
27 Doğrusal olarak ayrılamayan fonksiyonlar.
28 Marvin Minsky, Seymour Papert, An Introduction to Computational Geometry, Cambridge, 1969.
Şekil 14 NOT, AND, OR, XOR operatörleri için mantıksal doğruluk tablosu
Perceptron öğrenme algoritmasının en büyük eksikliği sadece doğrusal olarak ayrılabilen veriler üzerinde sınıflandırma yapabiliyor olmasıdır. AND ve ORproblemleri doğrusal özellik gösterir ve bu problemler perceptron ile çözülebilir.Fakat perceptronlar Minsky ve Papert’in işaret ettiği XOR problemi gibi doğrusal olarak sınıflandırılamayan problemlerin çözümünde başarısızdır. XOR fonksiyonu iki önerme arasındaki farklılık durumuna göre çalışır. Buna göre sonuçların aynı olması durumunda yanlış, farklı olması durumunda doğru çıktısını verir. XOR problemine göre tek katman ile bir yapay sinir ağının XOR fonksiyonunu sağlaması beklenemez. Çünkü XOR problemi doğrusal olarak ayrılabilen bir problem değildir yine de XOR problemi doğrusal fonksiyonlar kullanan perceptronlar ile çözülebilir. Yani verinin bulunduğu ortam üç boyutlu hale getirilirse iki sınıfı ayıran doğrusal bir düzlem bulunabilir.
Şekil 15. Veri üzerinde sınıflandırma yaparken boyut artırımının etkileri29
29 Cornell University, Machine Learning for Intelligent Systems, Lecture Noteshttp://www.cs.cornell.edu/courses/cs4780/2018fa/lectures/lecturenote03.html, 12 Aralık 2019.
3.3.3 Geriye Yayılım
Geriye yayılım (Backpropagation), çok katmanlı yapay sinir ağlarının eğitimi için kullanılan denetimli bir öğrenme algoritmasıdır. David Rumelhart (1942-2011), Geoffrey Hinton (1947- ) ve Ronald Williams’ın (1934- ) 1986'da yayınladığı30 bu algoritma çok katmanlı yapay sinir ağları üzerinde çalışmayı kolaylaştırmış ve Minskyile Papert’in dikkat çekmiş olduğu eksikliklerin bazılarının çok katmanlı ağlarda sorun oluşturmadığını göstermiştir. Geri yayılmalı öğrenme kuralı yapay sinir ağı çıkışındaki hata düzeyine göre her bir tabakadaki ağırlıkları yeniden hesaplamak için kullanılmaktadır. Böylece başlangıçta rastgele değerlerin atandığı ağırlık katsayıları, hata ortaya çıktığında geriye doğru en uygun değerle güncellenir ve böylece modeloptimize edilmiş olur. Bu tür yapay sinir ağları denetimli öğrenme kuralını kullanırlar yani bu işlem için hem giriş hem de çıkış verilerinin bilinmesi gerekmektedir.
30 D.E. Rumelhart, G.E. Hinton, R.J. Williams, “Learning Representations by Back-propagating Errors”,Nature Volume, 323, p. 533–536, 1986.
Şekil 16 Derin yapay sinir ağının eğitim aşamaları
Geriye yayılım algoritması, delta kuralı veya gradyan31 iniş olarak adlandırılan bir teknik kullanarak ağırlık alanındaki hata fonksiyonunun minimum değerini arar. Buna göre geriye yayılım algoritmasının 3 temel işlevi vardır. İlki sonucu hesaplamak için ilerleme işlemi, ikincisi hatayı geriye doğru yönlendirmek için gradyan alma işlemi, son olarak da bir optimizasyon algoritmasıyla parametrelerin güncellenmesi işlemidir.32
31 Hata sinyalinin girdilere göre alınmış kısmi türevlerine gradyan denir.
32 Toshinori Munakata, Fundamentals of the New Artificial Intelligence, Springer Science & Business Media, 2008, s.10-11.
Örneğin, görme problemlerini çözmek için eğitilmiş derin modellerde, en alt düzeyde yer alan nöronlar, kendi görme sistemimizde olduğu gibi, kenar, köşe ve renklere özelleşmiş durumdayken, orta düzeydeki nöronlar geometrik desenleri ve nesne parçalarını kodlarlar. Nesne veya sahne gibi soyut kavramların gösterimleri ise en üst katmanlarca yakalanır.
Önemle vurgulanması gereken bir diğer üstünlük ise aynı sinir ağı modeli ile hemen her türlü problemin çözülmesine olanak sağlanmasıdır. Konvansiyonel programlama tekniklerinde her tür problem için ayrı bir bilgisayar programına gereksinim duyulmasına karşılık, yapay sinir ağı modelinde problemin türüne göre ağ, sadece nöron sayısı ve ağırlıkların değişimine ihtiyaç göstermektedir.
Yapay sinir ağlarının mühendislik problemlerindeki en önemli üstünlüğü ise hesaplamaları direkt olarak deney sonuçlarını kullanarak öğrenmesi ve yapmasıdır. Diğer önemli üstünlüğü ise dağınık veya yetersiz veri olan problemlerde vetanımlanmış teorisi olmayan türden problemlerde kullanılması ve bu tür problemlerde doğruya yakın çözüm vermesidir.
3.3.4 Evrişimsel Sinir Ağları
Yapay sinir ağları ile görüntü tanıma, verilen bir görüntüyü önceden tanımlanmış kategorilerden birine sınıflandırma görevidir. Görüntü tanıma işlem aşamasında iki modül içerir bunlar öznitelik bulma ve sınıflandırmadır. Öznitelik bulma, ilgili kategoriler arasındaki farkı yakalayabilen ham piksel değerlerinden daha yüksek düzeyde ayrıntılı bilgi çıkarmayı içerir. Öznitelikler çıkarıldıktan sonra, görüntüler ve ilgili etiketlerle bir sınıflandırma modülü eğitilir. Bu eğitimde beklenen değerlere ulaşmak için istatistik (Lojistik Regresyon, Probit Regresyon, Poisson Regresyon, Genelleştirilmiş Katkı Modeli vb.) ve makine öğrenimi (K-En Yakın Komşu, Karar Ağacı, Destek Vektör Makinesi, Yapay Sinir Ağları vb.) algoritmalarından problem için en uygun olan kullanılır.
Görüntü tanımak için kullanılan geleneksel yapay sinir ağlarında sorun, bir görüntüyü sınıflandırmak ya da tanımak için tüm piksellerin nöral ağa aktarılması gerekmesidir. Bu işlemden kurtulmak için yapay sinir ağları geliştirilerek evrişimsel (convolutional) sinir ağları oluşturulmuştur.33 Evrişimsel ağlarda önce görüntüler üzerinde bazı örüntüler tespit edilmeye çalışılır ve bu örüntüler tekrar ağa aktarılırlar. Bu işlem için katmanlarının çıkışlarında, görüntüye dair öznitelik haritaları elde edilmektedir. Bu haritalarda ilk katmanlarda, kenar gibi daha basit bilgileri içeren öznitelikler tespit edilirken; daha üst seviyeli katmanlarda, ilk katmanlarda elde edilen öznitelikler kullanılarak görüntünün geneline ilişkin daha karmaşık öznitelikler çıkarılmaktadır. Böylece daha sade bir şekilde görüntünün işlenmesi ve başarı oranları yüksek sonuçların elde edilmesi sağlanabilmektedir.
33 Salman Khan, Hossein Rahmani, Syed Afaq Ali Shah, Mohammed Bennamoun, A Guide to Convolutional Neural Networks for Computer Vision, Morgan & Claypool Publishers, 2018, s.43.
Evrişimsel Sinir Ağları (Convolution Neural Network-CNN) çok katmanlı algılayıcıların kullanıldığı bir derin öğrenme mimarisidir. Evrişimsel sinir ağı yapısı ilkolarak Yann LeCun tarafından 1989 yılında yayınlanmıştır.34 1998 yılında yayınlananve ilk başarılı evrişimsel sinir ağı modeli olan LeNet-5 ise Yann LeCun ve ekibi tarafından posta numaraları, banka çekleri üzerindeki sayıların okunması için geliştirilmiştir.35 Rakamları sınıflandırabilen bu model, sistemin karşılaştığı sayının hangi rakamlardan oluşmuş olabileceğinin olasılıklarını kullanıcıya sunabilmekteydi.
Evrişimsel ağlarla sınıflandırma, örüntü tanıma, nesne tanıma alanlarındaki problemler için piksel tabanlı görüntü işleme yaklaşımları geliştirilmiş olsa da işlemcilerin yavaşlığı ve eğitim veri setlerinin boyutlarının yetersiz olması sebebiyle takip eden yıllarda; yeterli işlevselliğe ulaşılamamıştı.
2009 yılına gelindiğinde 3.2 milyon görüntü etiketlenerek elde edilen ImageNet isimli veri setinin oluşturması derin öğrenmenin potansiyelinin ortayaçıkmasına katkı sağlamıştır.36 Canlılardaki görsel algılama sistemi model alınarak geliştirilen bu yapılarda nöronlar tüm görsel üzerinde dağılmış şekilde alt bölgelere ayrılmıştır, basit hücreler, kenar/sınır çizgileri gibi özelliklere, karmaşık hücreler ise daha geniş alıcılarla, daha geniş alanlara yoğunlaşmaktadır. Bir evrişimsel ağ, bir veya daha fazla evrişim katmanı, ortaklama katmanı ve son olarak bir veya daha fazla bağlantı katmanından oluşur.
34 Y. LeCun,"Backpropagation Applied to Handwritten Zip Code Recognition", Journal Neural Computation, 1989, p. 541-551. (Çevrimiçi) http://yann.lecun.com/exdb/publis/pdf/lecun-89e.pdf,12 Aralık 2019.
35 Y. LeCun, “Gradient-Based Learning Applied to Document Recognition”, Proceedings of the IEEE, Volume: 86 , Issue: 11 , Nov 1998, s. 2278 - 2324.
36 Jia Deng, Wei Dong, Richard Socher, Li-Jia Li, Kai Li, Li Fei-Fei, “ImageNet: A Large-ScaleHierarchical Image Database”, Princeton University, USA, 2009. (Çevrimiçi)http://vision.stanford.edu/pdf/ImageNet_CVPR2009.pdf, 12 Aralık 2019.
Şekil 17 Evrişimsel sinir ağının katmanları37
Şekil 17 de görüldüğü gibi görüntü kare şeklinde parçalara ayrılır. Her bir parçaya boyutları genel görüntüden küçük ve aranan değere uygun filtreler (matris/kernel) uygulanır. Filtre işlemi sırasında evrişim (konvolüsyon) denilen matris çarpımları şeklinde sayısal hesaplamalar yapılır. Bu işlemler sonucunda elde edilen yeni piksel değerleri ortaklama (pooling) işlemiyle problemin özelliklerine bağlı olarak matristeki en yüksek değer ya da ortalama değer alınarak son katman oluşturulur.38
Toronto Üniversitesi’nden Geoffrey Hinton (1947-) ve ekibinin 2012 yılında oluşturdukları evrişimsel sinir ağı modeli AlexNet görsel tanımada doğruluk oranını %74,3’ten %83,6 seviyelerine çıkarmıştır.39 AlexNet görüntü tanıma problemi için bir kırılma noktası olarak görülmektedir. AlexNet’ten sonra 2016 yılına kadar geliştirilen farklı evrişimsel sinir ağı modelleri ve başarı oranları aşağıdaki grafikte görüldüğü gibi sürekli bir artış göstermiştir. Bu başarı oranlarının artmasında donanımsal gelişmeler, algoritmaların geliştirilmesi ve veri setlerinin hızla büyümesi gibi ilerlemeler etkili olmuştur.
39 A. Krizhevsky, I. Sutskever, G. E. Hinton, “ImageNet Classification with Deep Convolutional NeuralNetworks”, Advances in Neural Information Processing Systems-25, 2012.
37Stanfort Üniversitesi CS 230 - Deep Learning ders notlarından. (Çevrimiçi)https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-convolutional-neural-networks, 12 Aralık 2019.
38 Stanfort, A.e.
Şekil 18 2016 verileri ile oluşturulmuş evrişimli sinir ağı modellerinin başarı oranları grafiği40
40 Alfredo Canziani, Adam Paszke, Eugenio Culurciello, "An Analysis of Deep Neural Network Models for Practical Applications", ICLR 2017 conference, 2016.
3.3.5 Inception Sinir Ağları
Evrişimsel Sinir ağlarındaki hesaplama karmaşıklığını gidermek için 2013yılında yayınlanan “Network in Network”41 isimli makaleleriyle Min Lin ve ekibievrişimsel sinir ağının içine çok katmanlı algılayıcı yapısı ekleyerek yeni bir modelelde ettiler. Bu model temelde, aynı girdiye uygulanan havuzlama ve birden fazla evrişim işleminin ardı ardına uygulanması yoluyla çalışır. Bu özelliği sayesinde ağ, aynı anda hem genel hem de özel öznitelikleri çıkarabilmektedir.
41 Min Lin, Qiang Chen, Shuicheng Yan, “Network In Network”, Cornell University, ICLR 2013.
3.3.6 Kapsül Ağlar
Şekil 19 Inception Ağ Mimarisi42
Her ne kadar nesne tanımada evrişimli sinir ağları ile umut vadeden sonuçlar elde ediliyor olsa da evrişimli sinir ağları bazı problemleri beraberinde getirmektedir. Eğitilmiş evrişimli sinir ağı, üzerinde eğitilmiş olduğu nesne fiziksel olarak farklı bir açıdan görselleştirilmiş olduğunda aynı başarı ile tanıma işlemini gerçekleştirememektedir. Evrişimli sinir ağını bir nesneyi oluşturan parçaların arasındaki hiyerarşiyi (örneğin bir yüzün göz, ağız, burun vb. organlardan oluşması) çözümleyememektedir. Aynı zamanda evrişimli sinir ağlarındaki ortaklama işlemi ile gerçekleştirilen boyut azaltma da bilgi kaybına neden olmaktadır. Konum, yönelim, duruş ve açısal değerin değişmesi durumunda dahi bir grup yapay nörondan oluşan kapsüller aracılığıyla nesnenin başarıyla tanınabilmesi için nesneyi temsil eden kalınlık, ölçek, kaydırma vb. özelliklerin anlaşmalı yönlendirme ile öğrenilmesi önerilmiştir
Derin öğrenmenin kurucularından olan Geoffrey Hinton evrişimli ağlarda ortaya çıkan sorunların sebebinin ortaklama (pool) işlemi olduğunu ifade etmiş ve bu hatayı gidermek için 2018 yılında Kapsül Ağlarını (Capsule Networks) önermiştir.43 Kapsül ağlardaki derinliği, diğer yapay sinir ağlarında olduğu gibi katmanların art arda bağlılığı değil iç içe kapsüller sağlamaktadır. Kapsül ağ yapısı sayesinde, görüntülerin içerdiği hiyerarşik ilişkiler (öz niteliklerin ayrıntıları, bölgesel görüntülerin konumları vb.) daha verimli şekilde öğrenilmektedir.
42 Min Lin, Qiang Chen, Shuicheng Yan, “Network In Network”, Cornell University, ICLR 2013.
43 Geoffrey Hinton, Sara Sabour, Nicholas Frosst, “Matrix Capsules With EM Routing”, ICLR, 2018.(Çevrimiçi) https://openreview.net/pdf?id=HJWLfGWRb
Evrişimli sinir ağı modellerinde yaşanan bazı problemleri gidermesi beklenen kapsül ağları ile MNIST (Modified National Institute of Standards and Technology) veri seti üzerinde %99,75 başarı elde edilmiştir. Özellikle görüntüde konum, yönelim ve açı bilgisinin diğer derin öğrenme modellerine göre daha verimli44
44 Sabour, S., Frosst, N. ve Hinton, G.E., “Dynamic Routing Between Capsules'', arXiv preprint arXiv:1710.09829, 2017.
Görüntü tanımada ortaya çıkan sorunları giderebiliyor olmasına rağmen kapsül ağların geliştirilmesi gerekmektedir. Çünkü evrişimsel sinir ağı modeline göre işlem yükü daha fazladır ve bu yüzden de eğitilmesi daha uzun sürmektedir.
3.4 Beyni Modellemek
Yapay sinir ağlarının ilerleyişi ve başarılı sonuçlara ulaşılması sonucunda beynin çalışma sistemini makinelere aktarma fikri geliştirilmiştir. Beynin çalışma şeklini anlayabilmek ve ihtiyaç duyulan noktalarda yapay olarak onu oluşturup kullanabilmenin diğer teknolojik gelişmeler gibi birçok kolaylık sağlayacağı ileri sürülmektedir.
İnsan beyninin silikon tabanlı bir ortamda simülasyonunun oluşturulmasının hedeflendiği Mavi Beyin Projesi, IBM ve Brain Mind Enstitü tarafından İsviçre’deki Ecole Polytechnique Fédérale de Lausanne (EPFL) da devam etmektedir. Mavi Beyin Projesi ekibi, insan beynindeki sinir ağlarının karmaşıklığını açıklayabilmek için matematiksel bir dal olan cebirsel topolojiyi kullanmaktadır. Buna göre sinir ağları bağlantılarında ortaya çıkan karmaşıklık çok yüksek seviyelerde olmasına rağmen yine de bu bağlantıların tanımlanabileceği matematiksel bir zemin oluşturabilmek mümkün olabilir.
Projenin Frontiers in Computational Neuroscience dergisinde yayımlanmış sonuçlarına göre; tüm vücut hücrelerinden farklı olarak beyindeki hücreler on bir boyuta kadar etkinlik göstermektedir. Burada boyut kelimesiyle topolojideki simplekslerin karmaşıklığı ifade edilmektedir. Bir dizi sinir hücresi arasındaki bağlantılar bu simplekslerle temsil edilebilmektedir.45
Şekil 20 Sinir ağlarında görüntülenen simpleks örneği46
Proje ile topolojideki simpleksler model alınarak beyindeki nöronların bağlantışekillerini nesnel olarak sınıflandırmak için matematiksel bir algoritma geliştirilmekistanmektedir. Bu algoritma sayesinde araştırmacılar nöronlar ile ilgili edindikleri verileri karşılaştırabilecek ve algoritma ile beyindeki tüm hücrelerin standart bir sınıflandırılmasının yapılmasına olanak sağlanacaktır.47 Söz konusu gelişme sinir bilim çalışmalarında ilerleyebilmek için faydalı olabilir, çünkü daha gelişmiş bir hücre taksonomisi anlayışı ve güvenilir bir karşılaştırmalı yöntem sağlayacaktır. Morfolojik tiplerin nesnel tanımı, beynin temel yapı taşlarının daha iyi anlaşılması için gerekli ilk adımdır. Bu yöntem, tüm beyin bölgelerinin ve glia hücrelerinin nöronları dâhil olmak üzere beyindeki tüm hücre türlerinin tutarlı bir şekilde tanımlanması için kullanılabilir.
45 Henry Markham, Cliques of Neurons Bound into Cavities Provide a Missing Link between Structureand Function, June 12, Frontier, 2017, (Çevrimiçi) https://doi.org/10.3389/fncom.2017.000488, 12Aralık 2019.
46 A.e.
47 Objective Morphological Classification of Neocortical Pyramidal Cells, EPFL, Cerebral Cortex, Volume 29, Issue 4, Nisan 2019, s.1719–1735. (Çevrimiçi)https://academic.oup.com/cercor/article/29/4/1719/5304727, 12 Aralık 2019.
3.5 Hesaplama ve Oyun
Turing’in çalışmalarına, 1928 yılında ortaya koyduğu düşünceleriyle David Hilbert yön vermiştir. Matematiğin biçimselleştirilmesi için çalışmakta olan Hilbert özetle şunu söylemekteydi: eğer matematik nesnelse ve matematiksel bir ispat “doğru” ya da “yanlış” olarak betimlenebiliyorsa, bu ispatın doğru ya da yanlış olduğunu belirleyebilen kesin kurallar olmalıdır. Hilbert bir aksiyomlar kümesine ve biçimsel dile sahip olmayı önerdi. Bu biçimsel sistem, herkesin üzerinde anlaşabileceği ve bütün matematiksel akılyürütmeleri içerecek mükemmel bir sistem olacaktı. 1930’da Gödel böyle bir biçimsel sistemin var olamayacağını ispatlamıştı ardından Turing bu konuyu farklı bir açıdan ele alarak Turing Makinesi olarak anılan matematiksel modelini geliştirmiştir. Turing'in bu modeli, bazı matematiksel önermelerin yapısal olarak hesaplanamaz olduğunu, yani bu önermelerin doğru veya yanlış olduklarının matematiksel olarak gösteriminin olanaksız olduğunu ortaya koymuştur. 1940'larda ise bu matematiksel modelin sadece matematik problemlerini çözmek için geliştirilmiş bir model olmadığını; problem çözme olarak ifade edilen işlemi tanımlayan bir model olduğunu fark etmiştir. Buna göre bilimsel anlamda problem çözme işlemine hesaplama denmektedir ve insan beyninin geliştirdiği hesaplama işlemleri ile bilgisayarların geliştirdikleri hesaplama yöntemleri farklılıklar göstermektedir.
Bilgisayarların sahip olduğu hesaplama gücü teknolojik ilerlemeler sayesinde arttıkça Bu farklılıklar da daha gözlemlenebilir bir hal almıştır. Makinelerin satranç, Go, poker, StarCraft, DOTA gibi herhangi bir oyunda ya da herhangi bir görevde insanlardan daha başarılı olduğu birçok kez ispatlanmıştır. Bu oyunlarda insanlardan başarılı olmak için insanlardan daha az hata yapmak yeterlidir.
Daha yakından inceleyecek olursak dünya satranç şampiyonu Garry Kasparov’u satrançta yenen IBM’in bilgisayarı DeepBlue, bu maçta oynanabilecek tüm olasılıkların ve hamlelerin bir “ağacını” çıkarmış, bu karar ağacında bir tarama yapmış ve milyonlarca hamle arasından en uygun yani en büyük kazancı sağlayabileceği hamleyi seçmiştir. Buna göre, satrançta her durum için yapılabilecek yüzlerce hamleden ve her hamleye rakibin verebileceği yüzlerce cevaptan oluşan durum uzayı ele alındığında herhangi bir insanın böyle büyük bir hesaplama işini yapması mümkün değildir.
Deep Blue’nun Garry Kasparov’u yendiği 1997 yılı ile günümüz yapay zeka programlarının -donanımsal gelişmelerin dışında- en büyük farkı ise büyük eğitim verilerine sahip olunması ve makine öğrenmesi yöntemlerinde ortaya çıkan yeniliklerdir. Son yıllarda yapay zekâ alanında yaşanan önemli gelişmelerin arkasında bilgisayar biliminin ilk günlerinde ortaya atılan, yapay sinir ağları vardır. Yapay sinir ağları fikir olarak ortaya çıktığı ilk dönemlerde kullanışlı bulunmamıştı, çünkü karmaşıklıklarından dolayı eğitilmeleri uzun sürüyordu ve eğitim için gerekli olan veri çok sınırlıydı. Günümüzde bu dezavantajlar büyük ölçüde giderilmiş durumdadır. Yapay sinir ağları yoluyla gerçekleştirilen öğrenme yöntemleri, Deep Blue’nun ağaç taraması baz alındığında insanın öğrenme şekline daha fazla benzerlik gösterdiği düşünülmektedir. İnsanın akılyürütme bakımından en önemli özelliklerinden biri olan eksik bilgiye dayalı akılyürütme yapabilmesi ve gerektiğinde kararlarını hızlı bir şekilde güncelleyebilmesidir.48 Derin öğrenme yöntemlerini diğer makine öğrenmesi tekniklerinden ayıran en önemli yönü bu monoton olmayan akıl yürütme yöntemini daha büyük oranda yani her bir katmanda kullanabiliyor olmasıdır.
48 Vedat Kamer, "Feshedilebilir Akılyürütme", VI. Mantık Çalıştayı Kitabı, Kamer V., Ural Ş., Ed., Mantık Derneği Yayınları, İstanbul, ss.245-254, 2016 (Çevrimiçi)https://calistay.mantik.org.tr/wp-content/uploads/2017/01/VI-Mantik-Calistayi- Kitabi_DusukCozunurluk.pdf ,12 Aralık 2019.
2016’da dünya Go şampiyonu Lee Sedol’u yenen Google/DeepMind şirketinin AlphaGo isimli yazılımı da yapay sinir ağlarını kullanarak öğrenen bir sistemdir. Lee Sedol ile yapılacak maç öncesinde AlphaGo 30 milyon hamlelik bir veri setiyle eğitilmiştir. AlphaGo’nun eğitimi için kullanılan bu eğitim seti insan Go oyuncularının oyunlarından elde edilmişti. Maçtan sonra, DeepMind ekibi Go oyununda insan verisi kullanmadan kendi kendini geliştirebilen bir program yazma fikrini geliştirmişti. Bu yeni programda aynı öğrenme yöntemi kullanıldı fakat programa oyunun kuralları dışında herhangi bir bilgi verilmedi. AlphaGo Zero adı verilen bu program kendi kendine karşı milyonlarca maç yaptı ve böylece eğitim verisini kendisi oluşturmuş oldu. Kendi oluşturmuş olduğu veri seti ile eğitimini tamamlamasının ardından AlphaGo ve AlphaGo Zero karşı karşıya getirildi ve 100 oyunun 100’ünü de AlphaGo Zero kazandı.49 Böylece makinelerin geliştirdikleri problem çözme yöntemlerinin insanlardan çok farklı olabildiği ve insanlardan edinilmiş olan, insanın düşünme şeklini yansıtan, eğitim verisinin aslında bilgisayarları kısıtladığı anlaşılmış oldu.
49 Tara Mahfoud, Sam McLean, Nikolas Rose, Vital Models: The MAking and Use of Models in the Brain, Academic Press, 2017, s. 104.
Klasik makine öğrenmesi tekniklerinden farklı olarak derin öğrenme yöntemiyle öğrenen makineler sadece “hesaplama yapmak” olarak nitelediğimiz davranış biçimlerinin dışına çıkabilmekte ve bu tür oyunlar için bir bakıma nasıl daha başarılı olunabileceğine dair yol göstermektedir. Bununla birlikte günümüzde kullanılan teknolojiler ve algoritmalar sürekli gelişse de değişmeyen şey makinelerin veri kümeleri yoluyla eğitilmesi öğrenmesi olacak gibi görünmektedir.
SONUÇ
İnsan beyni aritmetik işlemleri kolaylıkla yapabiliyor olsaydı, zamanı hatasız bir şekilde ölçebilseydi, çok basamaklı sayılarla hızlı ve hatasız işlemler yapabilseydi hesap makinelerinin, saatlerin, takvimlerin ortaya çıkmasına ihtiyaç kalmazdı. İnsan beyni bu tür ölçümler ve hesaplamaları yapabilecek kadar gelişmiş olmamasına rağmen “anlama yeteneği” makinelerle değil insanlarla bağdaştırılır. Bu sebeple makinelerde anlama yeteneğinin geliştirilmesi için kullanılan doğal dil işleme tekniklerini de içeren makine öğrenmesi ilk olarak insan öğrenmesi model alınarak geliştirilmiştir.
İnsan beyninde oluşan anlam ve anlama yeteneğini tanımlayabilmek, bunların ortaya çıkması için beyinde gerçekleşen elektriksel etkinliği saptayabilmek ve analiz edebilmek için beynin biyolojik yapısı incelenmiştir. Beynin anatomisi üzerine yapılan bu tür araştırmalarda özellikle görsel sisteme ilişkin önemli bilgiler eldeedilmiştir. Gözle bağlantılı veri işleme sistemi görsel verileri analiz edip anlamlı halegetirirken neredeyse kusursuz bir performans göstermektedir. Bu veri analiz sürecinin incelenmesiyle, görsel sistemin, ışık ve renk birlikteliğinin ortaya çıkardığı görüntüleri analiz ederken, kendileri de kenar çizgileri tarafından sınırlanan iki boyutlu yüzeylerin sınırladığı nesneleri üç boyutlu uzayda algılamamızı sağlayan karmaşık bir yapısı olduğu ortaya çıkmıştır.
Görsel sistemin nesneler üzerindeki çizgisel ve dairesel sınırları temel alan yapısının, yapay sinir ağları kullanılarak taklit edilmesiyle de derin öğrenme gerçekleşir ve bir bilgisayar, milyonlarca fotoğraf ile eğitilerek belli bir nesneyiinsandan daha iyi tespit edebilecek seviyeye gelebilir.
Eski bir makine öğrenmesi yöntemi olan yapay sinir ağları, çok uzun bir süre pratik bir yöntem olarak görülmemiştir. Çünkü fazla karmaşık oldukları için eğitilmeleri çok uzun sürmekte ve buldukları bağlantılar mevcut eğitim verisi ilesınırlı kalmaktadır. Günümüzde bilgisayar işlemcilerinin gelişimi ve bilgisayarların eğitimi için ihtiyaç duyulan veri setlerinin büyüklüğü yapay sinir ağlarının dezavantajlarını büyük ölçüde gidermiş durumdadır. İşlemcilerin gelişmesi ve büyük veri setlerine erişilmesi çeşitli algoritmalarla bilginin işlenmesini ve analiz edilmesini daha da önemli hale getirmiştir.
Çalışmamızda da hesap makinelerinden yola çıkarak incelediğimiz bilgisayarların bu teknolojik gelişim sürecinde en önemli noktalardan biri bilgisayarların bilgiyi işleyişidir. Hızlı ve hatasız işlem yapmak gibi basit bir ihtiyaçtan dolayı ortaya çıkan bir araç olan hesap makinelerinin başka neler yapabileceği sorusu makineleri sürekli gelişmekte olan cihazlar haline getirmiştir. Bu gelişimin bir noktasında makinelerin bilgiyi depolayan ve kullanabilen araçlar haline gelmesi ile uzman sistemler ortaya çıkmıştır. Gelişmedeki bir sonraki aşama olan makine öğrenmesinde ise bilgi, veri setleri halinde bilgisayarlara aktarılmış ve bu veri setlerinden belirli problemler için belirli çözümler üretmesi yani çıkarım yapması sağlanmıştır. Derin öğrenme makineler için bilgiyi işleme çabasının geldiği son noktasayılmaktadır. Derin öğrenme sistemlerinin karar verebilmesi için büyük veri setlerini işleyip doğru şekilde yorumlaması gerekmektedir. Karar aşamasında insan zihninde gözlemlenen şey girdi ve çıktılar arasındaki nedensel ilişkidir. Buna göre zihin duyular yoluyla edindiği bilgiyi girdi olarak almakta ve bu duyusal bilgi pek çok farklı aşama ve düzeyde işlenmekte; sonrasında ise çıktı olarak bir davranış üretilmektedir. Bir bilgisayar programı da benzer şekilde girilen veriyi işleyerek bir çıktı üretmektedir. Yapay zihnin inşasına ilkece zemin hazırlayan bu yaklaşım işlevselci yaklaşım olarak bilinmektedir.
Bir bilgisayar programı ile zihin durumları arasında benzerlik olduğunu iddia eden işlevselciliğin göz ardı ettiği şey ise bilinç kavramı ve ona bağlı olarak kayıp deneyimsel nitelikler (absent qualia) argümanıdır. Bu argümana göre işlevsel olarak duyusal varlıkların kopyalarının üretilmesi mümkündür ancak bu kopyalar insanlar gibi deneyimsel niteliklere sahip olamazlar. Deneyimsel niteliklerin bilince işaretetmesi sebebiyle, bilincin gizemli bir fenomen olmaktan çıkması ancak deneyimleyen öznenin doğası hakkında açıklama sunan bir bilinç yaklaşımıyla son bulabilir.
İnsan beynindeki sinir hücreleri modellenerek geliştirilen derin öğrenme teknikleri sayesinde makineler işitme, konuşma, görme gibi insan duyusal deneyimlerini taklit etmede son derece başarılı olmuşlardır. İstatiksel çıkarım ve koşullandırma ile optimizasyon gibi yöntemleri kullanan derin öğrenme ağ modelleri özelleştirilmiş problemler üzerinde başarılı olsa da tüm problemler için genelleştirilmiş bir model oluşturulamamıştır. İnsan bilinci söz konusu olduğunda iseinsan beyninin bir bütün olarak tüm işlevselliği ve bu işlevselliğin farkında olma durumu göz önünde bulundurulmalıdır.
Bir makineye kazandırılmak istenen en belirgin özellik herhangi bir şeyi taklitetme yeteneğidir. Bu özellik sayesinde evrendeki en karmaşık yapı olduğu düşünülen insan beyninin de taklit edilebilmesi araştırılmaktadır. Beynin görme, öğrenme, bilgi işleme, hesap yapma vb. fonksiyonları taklit edilebilir olsa da, beyinde ortaya çıktığı düşünülen bilincin taklit edilmesinin önünde deneyimsel nitelikler engeli vardır. Öznel olan deneyimsel nitelikleri kapsayan bilinç, taklitedilebilir bir yapı olarak görülmemektedir.
Çalışmamızda makine öğrenmesi aşamasına kadar insan dışı bir ortamda bilgi işlemenin tarihsel gelişimini ortaya koyduk. Bu bilgi işleme sürecinin henüz bir bilinç olarak adlandırılmaktan uzak olduğunu gördük. Bu uzaklığın en önemli nedeni her insan bilincinde yer alan niteliksel yönün modellenmesiyle ilgili sorunlar görünmektedir. Yapay sinir ağları beyindeki biyolojik sinir ağlarının şimdilik bilimsel olarak bilinen bazı özelliklerini taklit etmeye çalışmaktadır. Bu nedenle insan beyninin büyük paralel işleme kapasitesiyle karşılaştırıldığında, yapay ağlar ancak basitleştirilmiş modeller sunmaktadır. Bu modellerin geliştirilebilmesi için yapayzekâ çalışmaları açısından araştırılması gereken en önemli soru, yapay sinir hücrelerinin, insan zekâsından da bağımsız olarak, zekâyı temsil edebilmek üzere ne tür özelliklere sahip olması gerektiğidir.
KAYNAKÇA
Alpaydın, Ethem: Introduction to Machine Learning, London: The MIT Press, 2004.
Anderson, James A.: Talking Nets: An Oral History of Neural Networks, Bradford Book, 2014.
Aydın, Süleyman: İnsan Anatomisi Ve Fizyolojisi, Anadolu Üniversitesi,2000.
Atherton, W. A.: From Compass to Computer: History of Electrical and Electronics Engineering, Macmillan International Higher Education, 1984.
Bauer, Craig: Secret History The Story of Cryptology, Chapman and Hall / CRC, 2013.
Berry, Michael: Azlinah Mohamed, Bee Wah Yap, Supervised and Unsupervised Learning for Data Science, Springer Nature, 2019.
Bennett, Deborah: Logic Made Easy, W.W. Norton & Co, 2004.
Bernhardt, Chris: Turing's Vision: The Birth of Computer Science, MIT Press, 2016.
Block, Ned: Troubles with functionalism, Minnesota Studies in the Philosophy of Science 9:261- 325,1978.
Bodur, Aydın: Shannon'a Saygı, Elektrik Mühendisleri Odası,2010.
Bornet, I. G. Gerard: George Boole: Selected Manuscripts on Logic and its Philosophy, Springer Basel AG, 1997, s. 30.
Chaitin, Gregory: Thinking about Godel and Turing: Essays on complexity, 1970-2007,World Scientific Publishing Company, 2007.
Churchland, Patricia&P: Could a Machine Think? , Scientific American Ocak,1990. (Çevrimiçi)http://sils.shoin.ac.jp/~gunji/AI/CR/sciam90couldamac hinethink.pdf, 12 Aralık 2019.
Cohen, Daniel: Equations from God: Pure Mathematics and Victorian Faith (Johns Hopkins Studies in the History of Mathematics), The Johns Hopkins University Press, 2007.
Daniel, Grape: Principles Of Artificial Neural Networks: Basic Designs To Deep Learning, World Scientific, 2019.
Descartes, Rene: İlk Felsefe Üzerine Metafizik Düşünceler, (Çev. Mehmet Karasan), MEB Yayınları, İstanbul,1998.
Elfadel, Ibrahim: Duane S. Boning, Xin Li, Machine Learning in VLSI Computer-Aided Design, Springer, 2019.
Gertner, Jon: The Idea Factory: Bell Labs and the Great Age of American Innovation, Penguin, 2012.
Gödelek, Kamuran: Zihin Felsefesi, Eskişehir: Anadolu Üniversitesi Yayınları, 2011.
Grier, David Alan: When Computers Were Human, Princeton University Press, 2013.
Gür, Bekir: Leibniz’in Matematik(sel) Düşüncesi, MatematikDünyası, 2005 Güz.
Hardie, D.G.: Biochemical Messengers: Hormones, Neurotransmitters and Growth Factors, Springer Science & Business Media, 1991.
Hays, Sean: Jason Scott Robert, Clark A. Miller, Ira Bennett,Nanotechnology, the Brain, and the Future, Springer Science & Business Media, 2012.
Hebb, Donald: The Organization of Behavior, Psychology Press, 1949.
Herbert, Joe: The Minder Brain: How Your Brain Keeps You Alive, Protects You from Danger, and Ensures that You Reproduce, World Scientific, 2007.
Hinton, Geoffrey: “Matrix Capsules With EM Routing”, ICLR, 2018.(Çevrimiçi)https://openreview.net/pdf?id=HJWLfGWRb, 12 Aralık2019.
Hofstadter,DouglasR: Aklın G'özü: Benlik ve Ruh Üzerine Hayaller ve Düşünceler (Çev: Füsun Doruker), Boğaziçi Üniversitesi Yayınevi, 2005.
Hiller,D.E.Hyndman: AnalogandHybridComputing,PergamonPress,1970.
Ifrah, Georges: Rakamların Evrensel Tarihi: Akdeniz Kıyılarında Hesap, Tubitak Yayınları, 1995.
Jefferson, G.: The Mind of Mechanical Man, Lister Oration for 1949, British Medical Journal, 1949.
John,Locke: İnsan Anlığı Üzerine Bir Deneme, (çev. Vehbi Hacıkadiroğlu), Kabalcı Yayınevi, İstanbul, 1992.
Kamer, Vedat: Feshedilebilir Akılyürütme, VI. Mantık Çalıştayı Kitabı, Mantık Derneği Yayınları, İstanbul, 2016(Çevrimiçi) https://calistay.mantik.org.tr/wp- content/uploads/2017/01/VI-Mantik-Calistayi- Kitabi_DusukCozunurluk.pdf, 12 Aralık 2019. “Yapay Zekâ ve Monoton-olmayan Mantık”,İstanbul Üniversitesi, 2009. (Çevrimiçi) http://acikerisim.istanbul.edu.tr/bitstream/han dle/123456789/27879/45445.pdf?sequence=1 &isAllowed=y, 12 Aralık 2019.
Khan, Salman: Rahmani, Syed Afaq Ali Shah, Mohammed Bennamoun, A Guide to Convolutional Neural Networks for Computer Vision, Morgan & Claypool Publishers, 2018.
Kouneiher, Joseph: Foundations of Mathematics and Physics One Century After Hilbert: New Perspective, Springer, 2018.
Leibniz, G. Wilhelm: G. W. Philosophical Essays (Çev: R. Ariew & D.Garber), Hackett Publishing Company, 1989. New Essays On Human Understanding, (Der. P. Remmant J. Bennet), New York: Cambridge University Press, 1997.
Lin, Min : “Network In Network”, Cornell University, ICLR 2013.
Mahfoud, Tara: Sam McLean, Nikolas Rose, Vital Models: The Making and Use of Models in the Brain, Academic Press, 2017.
Martin, Eddie: Computer Jargon Dictionary and Thesaurus, Beecroft Publishing, 2006.
McCarthy, John: "Programs with Common Sense", Teddington Conference on the Mechanization of ThoughtProcesses, 1958. (Çevrimiçi) http://www-formal.stanford.edu/jmc/mcc59.pdf, 12 Aralık 2019.
McFarland, T. D.: Expert Systems in Education and Training, Technology, Educational 1990.
Mehra,Jagadish: Einstein, Hilbert, and the theory of gravitation, D.Reidel Publishing Company, 1974.
Menabrea, L. F.: Sketch of The Analytical Engine Invented by Charles Babbage, Çev. Ada Lovelace, 1842. (Çevrimiçi)http://www.fourmilab.ch/babbage/sketch.html#Note G, 12 Aralık 2019.
Munakata, T.: Fundamentals of the New Artificial Intelligence, Springer Science & Business Media, 2008.
Nahin, Paul J: The Logician and the Engineer, How George Boole and Claude Shannon Created the Information Age,Princeton University Press, 2013.
Nagel, Thomas: What Is It Like to Be a Bat? Philosophical Review, 83 (4), 1974. Her Şey Ne Anlama Geliyor? (Çev. H. Gündoğdu). İstanbul: Paradigma Yayınları, 2004. Zihin ve Evren (Çev. Ö. Ç. Aksoy), İstanbul: Jaguar Kitap, 2015.Bernoulli Sayıları Üzerine, Matematik Dünyası,2009.
A Brief History of Computing, Springer Science & Business Media, 2012.
The Emperor's New Mind: Concerning Computers, Minds, and the Laws of Physics, Oxford University Press, 2016.
A Logical Calculus of Ideas Immanent in Nervous Activity,
1943. (Çevrimiçi)
https://www.cs.cmu.edu/~./epxing/Class/10715/reading/McC ulloch.and.Pitts.pdf, 12 Aralık 2019.
Theory Of Computation, Technical Publications, 2009.
Systematic Introduction to Expert Systems: Knowledge Representations and Problem-Solving Methods, Springer Science & Business Media, 2012.
Milestones in Computer Science and Information Technology, Greenwood Publishing Group, 2003.
Nesin, Ali:
O'Regan, Gerard:
Penrose, Roger:
Pitts, Walter:
Puntambekar, A.A.: Puppe, Frank:
Reilly, Edwin :
Roselló, Joan: Göttingen and the Development of ModernMathematics, Cambridge Scholars Publishing, 2019.
Rosenblatt,Frank: The Perceptron A Perceiving And Recognizing Automaton, 1957.
Ruiz, Francisco: Pablo Suau Pérez, Boyán Ivanov Bonev, Information Theory in Computer Vision and Pattern Recognition, Springer-Verlag London, 2009.
Russell, Stuart: Peter Norvig, Ernest Davis, Artificial Intelligence: A Modern Approach, Prentice Hall, 2010.
Salcedo, Jesus: Machine Learning for Data Mining, Packt Publishing, 2019.
Samuel, Arthur L.: Some studies in machine learning using the game of Checkers, IBM Journal of Research and Development, 1959.(Çevrimiçi)http://www.cs.virginia.edu/~evans/greatworks/samuel1959.p df
Say, Cem: 50 Soruda Yapay Zekâ, Bilim ve Gelecek Kitaplığı,2018.
Sayan, Erdinç: Bilinç, Felsefe Ansiklopedisi, c. 2, (ed. Ahmet Cevizci),Etik Yayınları, İstanbul, 2004.
Searle,John: Minds, Brains, and Programs, The Behavioral and Brain Sciences, 1980.
Sejnowski, Terrence: The Deep Learning Revolution, The MIT Press Cambridge, 2018.
Sertöz, Ali Sinan: Önce Matematik Vardı: George Boole, Bilim veTeknik, Aralık 2015.
Shannon, C. E.: A mathematical theory of communication, The Bell System Technical Journal- Nokia Bell Labs, 1948.
Shen, Alexander: Algorithms and Programming: Problems and Solutions, Springer Science & Business Media, 2011.
Shepherd, Gordon M.: Foundations of the Neuron Doctrine, Oxford University Press, 2015.
Soni, J & Goodman, R: A Mind at Play: How Claude Shannon Invented the Information Age, Simon and Schuster,2017. Zihnin Yeniden Keşfi, Çev. M. Macit, İstanbul: Litera Yayıncılık, 2004. Bilincin Gizemi, Çev. İ. K. İçyüz, İstanbul: Küre Yayınları,2018. Is the Brains Mind a Computer Program? , Scientific American, 1990.
Sra, Suvrit: Sebastian Nowozin, Stephen J. Wright, Optimization for Machine Learning, MIT Press, 2012.
Tomkins, Stephen: The Origins of Humankind, Cambridge University Press, 1998.
Toumey, Chris: Nanotech and the Humanities: An Anthropologist Observes the Science of Atoms and Molecules,Cambridge Scholars Publishing, 2019.
Turing, Alan M:Computing Machinery and Intelligence, Mind 49, 1950, s. 433-460. (Çevrimiçi)https://www.csee.umbc.edu/courses/471/papers/turi ng.pdf, 12 Aralık 2019. On Computable Numbers, With An Application To The Entscheidungsproblem, 1936. (Çevrimiçi)http://www.cs.virginia.edu/~robins/Turing_Paper_193 6.pdf, 12 Aralık 2019.
Alan M. Turing: Centenary Edition, Cambridge University Press, 2012.
Exploring Perceptual Illusions in Deep Neural Networks,Department of Psychology, University of Wisconsin – Madison,https://www.biorxiv.org/content/10.1101/687905v1.full, 12Aralık 2019.
“Santiago Ramon y Cajal ve Nöron Doktrini”, Turk JNeurol, 2015, Sayı:21, s.81-84. (Çevrimiçi)https://www.journalagent.com/tjn/pdfs/TJN_21_3_0. pdf, 12 Aralık 2019.









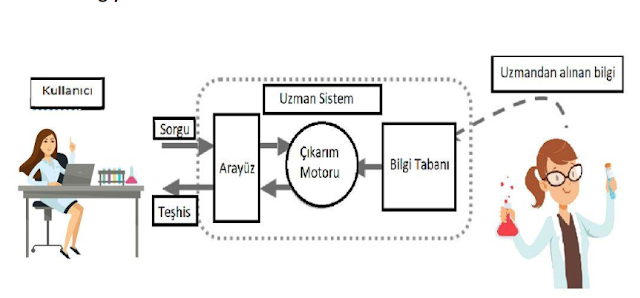


































0 Yorumlar